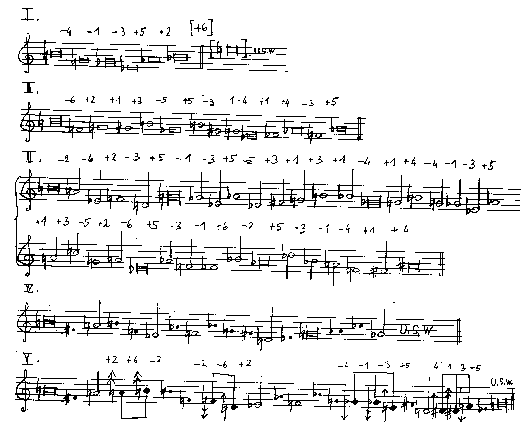
Abb. 6: Iterative Diminution aus 'Brüche': Konstruktionsplan
Die Länge der Reihe wächst dadurch exponentiell. Deshalb habe ich bisher auch meist nur 3 5 Iterationsebenen verwendet, was immerhin zu Reihenlängen von über tausend Tönen führte. Diese Iterationsebenen legen in der Realisation eine musikalischstrukturelle Abschattung nahe, um die Vielschichtigkeit des Ergebnisses auch hörbar zu machen.
In diesem Vorgang wird, so meine ich wenigstens, die Affinität zu den Iterationen der Patterngeneratoren bei Mandelbrot besonders deutlich.
Das folgende Beispiel zeigt 5 Interationsebenen aus 'Brüche' (Abb. 6 und 7). Als Substitutionstabelle wurde für Iteration IIV verwendet:
| Summe | Ordnung | Ersetzung |
| -4 -1 -3 5 2 6 |
2 3 4 2 2 3 |
[-6 2] [1 3 -5] [-4 1 3 5] [1 4] [-3 5] [2 6 -2] |
Für die V. Iteration wurden Mikrointervalle zur Diminution verwendet.
Die Substitutionstabelle lautet:
| Summe | Ordnung | Ersetzung |
| -12(4) -3(-1) -9(-3) 15(+5) 6(+2) 18(+6) |
4 -4 5 4 3 5 |
[-4 -1] + [-2 -5] [-4 -1 -3 5] [1 3 -5 -2 -6] [5 2] + [2 6] [2 6 -2] [1 4] + [5 2 6] |
Die V. Iteration wurde in Abb.6 aus Platzgründen nicht mehr vollständig ausgeführt.
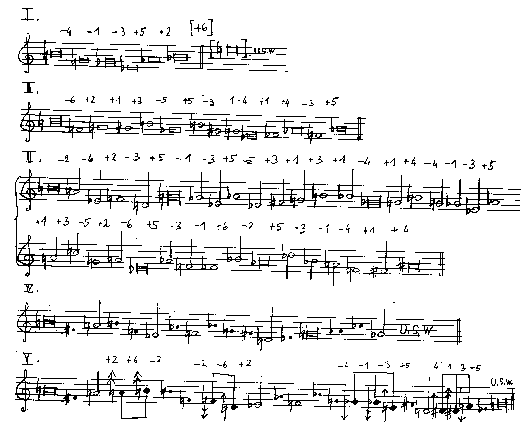
Hier wird mit Sechsteltönen
substituiert. Die halbtönigen Intervalle werden dementsprechend
verdreifacht. In der Substitutionstabelle nicht auftretenden
Intervalle werden durch Addition mehrerer ersetzbarer Intervalle
diminuiert.
Die deterministische
Verwendung obenstehender Substitutionstabelle führte zu
folgenden musikalischen Ergebnissen (ein Beispiel einer
Klarinettenstelle aus ´Brüche´ soll einen Diminutionsvorgang
mit Lizenzen verdeutlichen):

6.
Strukturelle Darstellung der Iterationsebenen
Um die Iterationsebenen
unterschiedlich darstellen zu können, bieten sich verschiedene
Möglichkeiten an:
| Iterationsebene 0 | ---> | metrische Teilung | 1:4 |
| Iterationsebene 1 | ---> | metrische Teilung | 1:5 bzw. 1:10 |
| Iterationsebene 2 | ---> | metrische Teilung | 1:6 bzw. 1:12 u.s.f |
| Iterationsebene 0 | ---> | pppppp bis ppp |
| Iterationsebene 1 | ---> | ppp bis p |
| Iterationsebene 2 | ---> | p bis mf |
| Iterationsebene 3 | ---> | mf bis f |
| Iterationsebene 4 | ---> | f bis ff |
Ebenso denkbar ist eine Umkehrung der Zuordnung, also die Iterationsebene 0 mit den f/ff Werten zu belegen.
| Iterationsebene 0 | ---> | Teilung pro Oktave | 1:12 ( Halbtöne) |
| Iterationsebene 1 | ---> | Teilung pro Oktave | 1:24 (Vierteltöne) |
| Iterationsebene 2 | ---> | Teilung pro Oktave | 1:48 (Achteltöne) |
Die
Substitutionsmöglichkeiten schränken sich bei dieser Wahl
natürlich ein.
Das Intervall 3 (kleine Terz)
der Iterationsebene 0 würde einem Intervall 6 (sechs
Vierteltöne) der Iterationsebene 1 entsprechen. Es kämen dann
alle Substitutionen für den Wert [6] in Frage. In der Achteltonebene
käme es zu einer weiteren Verdopplung der Ausgangswerte, was
hier schon zum relativ ungünstigen Wert [12] führen würde.
Spätestens hier muß der Einwand auftreten, ob es sich bei dem beschriebenen Verfahren nicht einfach um ein neoserialistischens Paradigma handle. Als Ausgangspunkt würde ich diese Klassifikation bejahen, doch in der Dynamik des Iterationsvorganges kann es zu einer neuen Auffassung der Serie an sich kommen, die als Metaserie
a) die Merkmale einer
Binnenkontrapunktik zeigt, also in sich kein einschichtiges
Gebilde darstellt,
b) sich nicht auf
dodekaphonische Vollständigkeit und Komplementarität
beschränkt,
c) authentisch in ihrem Umgang
mit richtungsgleichen Intervallen sein kann,
d) verschiedene Freiheitsgrade
des Komponierens simultan integrieren kann,
e) deren Umfang sehr groß
werden kann,
f) und die letztlich auch
harmonische Deutungen zuläßt.
Andererseits läßt sich das
Verfahren bei einer strengen Konzeption der Diminutionsregeln als
serielles Verfahren verstehen, d.h., sie schließt diese Deutung
nicht aus, kann sie aber vielleicht erweitern.
Ich sehe so etwa die
Möglichkeit, unter Verwendung deterministischer Prozesse einen
Zufallsgenerator im Sinne Cage´s zu schaffen, vor allem bei
Erzeugung größerer Tonmengen. Durch mehrfache Iteration läßt sich
der Tonraum sehr schnell mit Klangmassen ausfüllen, was
besonders unter Verwendung von Mikrointervallik einer Annäherung
an das Rauschen entspricht.
7.
Harmonische bzw. vertikale Diminutionen
Bislang wurde nur die
Diminution von Sukzessivintervallen diskutiert. Dadurch laßt
sich eine 'selbstähnliche' Struktur in der
horizontal-melodischen Dimension herstellen. Es stellt sich nun
die Frage, ob der gleiche Vorgang in der vertikalharmonischen
Dimension ebenfalls zu bewerkstelligen ist.
Die Ausgangsreihe laßt sich zunächst auf verschiedene Weisen seriell harmonisch interpretieren:
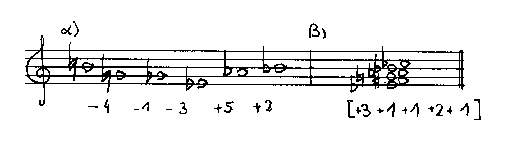
 ABB.9:
Positivintervallakkord der Reihe [-4-1-3+5+2]
ABB.9:
Positivintervallakkord der Reihe [-4-1-3+5+2]
 ABB.10: Akkord aus den
Absolutbeträgen der Reihe [-4-1-3+5+2]
ABB.10: Akkord aus den
Absolutbeträgen der Reihe [-4-1-3+5+2]
| 297.14 c | 408.57 c | 334.29 c | 185.71 c | 74.29 c |
Hier liegt bereits ein
Beispiel für eine vertikale Diminution vor. Die Centwerte
könnten einem Zwölfteltonsystem angenähert werden, um sie in
Notenschrift darstellbar zu machen.
Der Einfachheit wegen führe
ich hier ein weiteres Beispiel an, bei dem die
Proportionalteilung ganze Centwerte ergibt und das somit in
traditioneller Notenschrift darstellbar ist.
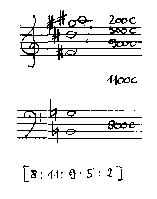 ABB.11: Akkord aus den
Proportionen der Positivintervalle
ABB.11: Akkord aus den
Proportionen der Positivintervalle
| 346.67 c | 86.67 c | 260 c | 433.33 c | 173.33 c |
Das folgende Beispiel zeigt eine Approximation der Proportionsreihe mit Sechsteltonintervallen bei einem Rahmenintervall von 3500 cent:
 ABB.12: Akkordteilung mit
den Proportionen der Absolutbetragsreihe
ABB.12: Akkordteilung mit
den Proportionen der Absolutbetragsreihe
Bei den letzteren Formen handelt es sich bereits um extreme Abstraktionen der Ähnlichkeitsbeziehungen.
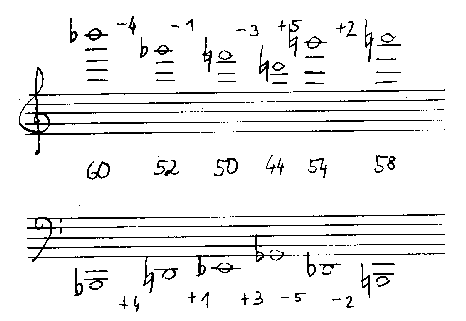
Die Formalisierung dieses Vorganges ist mir noch nicht befriedigend gelungen, weil die algorithmische Durchführung sehr komplex sein muß, wenn sie nicht zu trivialen Lösungen führen soll.
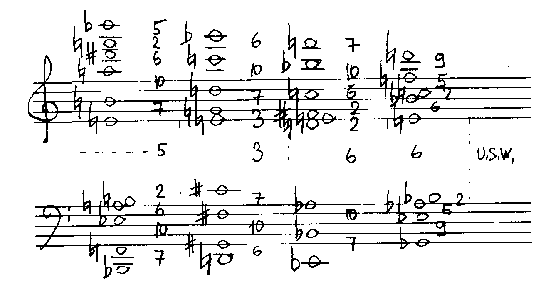
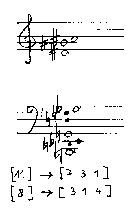 ABB.15: Beispiel für eine
iterierte harmonische Diminution: Die schwarzen Noten zeigen die aus der
letzten Iteration hervorgegangenen Töne. Der Ausgangsakkord
findet sich in der Abb. 9
ABB.15: Beispiel für eine
iterierte harmonische Diminution: Die schwarzen Noten zeigen die aus der
letzten Iteration hervorgegangenen Töne. Der Ausgangsakkord
findet sich in der Abb. 9
8.
Kombinationen von horizontaler und vertikaler Diminution: Die ´Raumfüllende
Linie´
Die Vorstellung einer
harmonischen Matrix wurde wesentlich durch die Konzeption des
Hauerschen Zwölftonspiels einerseits, durch die
Registrierungsharmonik Weberns andererseits angeregt. In beiden
Modellen erschien es mir immer merkwürdig, daß die
Ähnlichkeitsrelationen im vertikalen Bereich, nämlich der
konstante Bezug auf die regelmäßige Abfolge von zwölf
Tonhöhen-Klassen, im vertikalen Bereich chromatischen Bildungen
bzw. Terzenstrukturen gegenüberstanden, die auf diese Abfolge
keine Rücksicht nahmen. Aus dieser Überlegung heraus hatte ich
versucht, auch die Akkorde mit einem reihenähnlichen- oder
verwandten Intervallrepertoire zu füllen.
Diese harmonischen
Diminutionen haben bereits gezeigt, daß sich die Trennung
zwischer linearer und vertikaler Betrachtungsweise in der Matrix
aufhebt. Daraus ergibt sich die Frage, ob sich eine weitere Diminutionsform
finden ließe, die melodische mit harmonikaler Diminution
kombinierte. Diese Diminution müßte sowohl die Intervalle der Akkorde
mit der Ausgangsreihe ähnlichen oder gleichen Intervallfolgen ausfüllen
als auch im Melodieverlauf auf einer der beschriebenen
selbstähnlichen Diminutionen beruhen.
Der Determinationsgrad einer solchen Linie wäre nunmehr sehr hoch, die Lösungsmenge kann demnach nur sehr klein sein. Man könnte exakte Lösungen mit einem entsprechenden Suchprogramm finden. Gibt es keine derartige Lösung, so empfiehlt es sich praktisch, die resultierende Linie durch Ähnlichkeitstransformationen einzupassen, etwa durch:
Hier soll eine bloß schematische Skizze den Vorgang verdeutlichen:
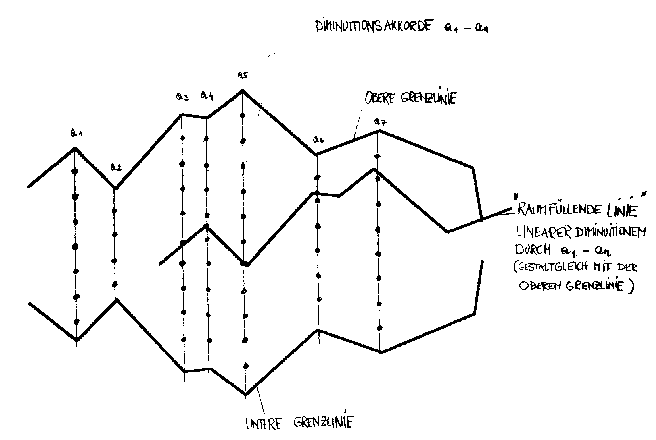
Die beiden dicken äußeren Linien repräsentieren die Grenzlinien, den Gerüstsatz der harmonischen Matrix. Beide sind aus einer selbstähnlichen iterativen Diminution hervorgegangen. Die vertikalen Strich - Punkt - Linien symbolisieren die Akkorde aus der harmonischen Diminution des Gerüstsatzes. Die dicke Linie zwischen den Grenzlinien zeigt eine kombinierte Diminution, die sowohl eine lineare Diminution durchführt als auch die Punkte der Akkordmatrix (annähernd) berührt.
Eine solchermaßen gewonnene Struktur hat die Eigenschaft, im strukturellen Hintergrund unter allen (musikalischen) Gesichtspunkten Ähnliches oder Gleiches zu zeigen, gleichzeitig aber im Vordergrund größte Vielfalt erscheinen zu lassen, was ja der Ausgangspunkt der Überlegungen war.21
------------------------------------------------------------
19 Das gilt auch für die folgenden Beispiele in 7.1.3, 7.1.4, 7.1.5.
20 Hier wird zunächst aus Gründen der Transparenz ein vereinfachter Fall dargestellt: näich daß die Einzelstimmen
nicht die Zeilen wechseln, also ohne Stimmkreuzungen gesetzt sind.
21 Vgl. Abschnitt 3.2