Peter Fleissner und Gregor Fleissner

Vorbemerkung

Spätestens seit dem Bau der ersten elektronischen Rechner fasziniert die Frage, ob Maschinen denken können. Die Diskussion darüber war und ist auch heute noch von mannigfaltigen Veränderungen der Interpretation der Begriffe "Denken" oder "Intelligenz" begleitet. Von 1950 bis in die frühen 80er Jahre setzte der Turing-Test eine praktisch nachprüfbare Grenze, ob eine Maschine menschliches Intelligenzniveau erreicht hat. Im Sinne behavioristischer Theorie wurde danach eine Maschine "intelligent" genannt, wenn eine Person (ein Nichtexperte), die über ein Terminal kommuniziert, durch Befragung nicht mehr feststellen kann, ob sich hinter dem Terminal ein Mensch oder ein Computer verbirgt (Turing 1950). Es ist klar, daß der bestandene Test nicht heißt, daß Maschinen im menschlichen Sinn denken können, sondern nur, daß sie ein Verhalten zeigen, das sich auf der Ebene textueller Interaktion von menschlichem Verhalten kaum mehr unterscheiden läßt (ein mit einem Schraubenzieher bewaffneter Techniker würde sich durch eine noch so perfekte Imitation menschlicher Schreibart nicht von einer Maschine täuschen lassen - er würde einfach nachsehen, was sich hinter dem Schirm befindet).

Im Jahre 1982 wurde der Turing-Test und seine spezielle Auffassung von maschineller Intelligenz durch den Philosophen John Searle herausgefordert (Searle 1982, 1990). In einem Gedankenexperiment, das als das "Chinesische Zimmer" in die Geistesgeschichte einging, beschrieb Searle ein System, das den Turing-Test in bezug auf das Verständnis der chinesischen Sprache bestehen würde. Searle selbst befindet sich in seinem Gedankenexperiment in einem Raum, der mit Kärtchen auf chinesisch und mit Indexkarten gefüllt ist, auf denen Instruktionen in englisch geschrieben sind. Durch eine Öffnung in der Wand wird Searle, der uns versichert, daß er keine Ahnung von chinesisch hat, ein chinesischer Text durchgereicht, und danach Zettel, die - wieder auf chinesisch - Fragen zu diesem Text enthalten. Im Lauf der Zeit entwickelt Searle - eingesperrt in das chinesische Zimmer - genügend Geschick, aufgrund der Instruktionen in englisch diejenigen Kärtchen herauszureichen, die richtige Antworten auf chinesisch auf die auf chinesisch gestellten Fragen enthalten. Heißt die Tatsache, daß Searle im Experiment auf chinesische Fragen die richtigen Antworten in chinesisch gibt, daß er selbst chinesisch versteht? Obwohl der Turing-Test als bestanden angesehen werden muß, meint Searle, daß er selbst nach wie vor kein Wort chinesisch verstünde, und weiters verallgemeinert er: "... and neither does any other digital computer because all the computer has is what I have: a formal program that attaches no meaning, interpretation, or content to any of the symbols" (Searle 1982).

Searle beantwortet mit seinem Gedankenexperiment die Frage nach der Denkfähigkeit von Maschinen durch eine Engführung des Begriffs Intelligenz. Durch seine Wahl der Fremdsprachenkenntnisse als speziellem Beispiel glaubt er, die inneren Fähigkeiten (des Verständnisses von Sprache) von der Anwendung dieser Fähigkeiten (korrekte Beantwortung von Fragen) abtrennen zu können (Turkle 1995: 87). Sprachverständnis und das Beantworten von Fragen können (so interpretieren wir Searle) in seiner Sicht als voneinander unabhängige Aktivitäten aufgefaßt werden. Damit weist er der Maschine zu, was der Maschine, und dem Menschen, was des Menschen ist. Die Ordnung der Dinge ist wiederhergestellt. Jedes hat seinen ihm zukommenden Bereich, und der Mensch wird beruhigenderweise durch die Maschine nicht entthront.

Obwohl wir die Schlußfolgerung von Searle (die man vielleicht respektlos so ausdrücken kann, daß ein Computer eben kein Mensch ist) klarerweise teilen, sehen wir in seinem Gedankenexperiment zwei - einander entgegengesetzte - Fehleinschätzungen: Die erste besteht in einer eher reduzierten Sicht des Problems der Fragenbeantwortung, wobei er den Computer und seine Möglichkeiten überschätzt. Wir wissen heute, daß es praktisch nicht möglich ist, ein vollständiges Set von Instruktionen für die Beantwortung von Fragen in befriedigender Weise anzugeben, immer kann uns eine Metafrage aus dem programmierten Korsett werfen. Dem entsprechend sind nach wie vor die Ergebnisse von Übersetzungsprogrammen ohne menschliche Bearbeitung nur eingeschränkt brauchbar, was nicht heißt, daß sie in speziellen Fällen und Disziplinen nicht eine wichtige Unterstützung menschlicher Arbeit darstellen können. Auch die Grenzen der Anwendung von Expertensystemen, etwa bei Vorhandensein von "tacit knowledge", weisen auf diese Schwierigkeiten hin.

Andererseits zeigt sich Searle zu pessimistisch und unterschätzt die Möglichkeiten des Computers, "to attach meaning, interpretation, or content to any of the symbols". Der vorliegende Beitrag entfaltet ein Gegenbeispiel, das zeigen soll, daß in bestimmten Settings auf dem Computer durchaus so etwas wie "Bedeutung" und "Pragmatik" entstehen kann, ja, daß die von Searle erwähnten "Instruktionen" durchaus nicht explizit vom Programm vorgegeben sein müssen, sondern daß sie sich erst im Lauf eines besonderen Interaktions- und Kommunikationsprozesses herausbilden können. Anders als bei menschlicher Kommunikation - und das ist die Einschränkung und der wesentliche Unterschied - ist allerdings die Menge der Symbole, die den virtuellen Subjekten des Programms insgesamt zur Verfügung steht, vom Programm vorgegeben. Welche allerdings davon ausgewählt werden, und welche Bedeutung sie erhalten, ist nicht voraussagbar.

Bei menschlicher Informationsverarbeitung ist die Menge der Symbole nur in reduzierten Fällen vollständig angebbar. Das Neue, das per definitionem nicht vorherzusehen ist, kann daher auch nicht als Element einer Menge angegeben werden, wie es die formale mathematisch-logische Behandlung erfordern würde.

Zur Konstruktion eines Gegenbeispiels zu Searles Auffassung werden anhand dieses Computerprogramms bestimmte Aspekte von Selbstorganisation simuliert, die - wie wir meinen - dadurch besser verstanden und präzisiert werden können, insbesondere das Zusammenspiel von Vorgängen zwischen physischer und symbolischer Welt (Pragmatik) sowie die Entstehung von Semantik durch diese Interaktion. Das Modell wurde von den Paradigmata der "Körperbasierten Artificial Intelligence", der "Emergent AI" (Turkle 1994: 125-148) und dem Setting der Freudschen Psychoanalyse inspiriert . Zur besseren Einordnung des hier beschriebenen Verfahrens wird das Modell mit der Lernmatrix von Steinbuch verglichen.

Das Szenario

Wir treffen einige allgemeine Voraussetzungen, die darstellen sollen, von welchem Blickwinkel aus das Modell aufgebaut wurde. Wir unterscheiden eine physische Welt, Welt A, die durch physikalische Gesetze vollständig beschrieben werden kann, von einer informatischen Welt, Welt B.

Jede Ursache besitzt in Welt A eine ihr eindeutig zugeordnete Wirkung. Diese Welt ist die (wie wir heute wissen, eingeschränkte Sicht der) Welt der klassischen Mechanik, actio est reactio.

Die zweite Welt, Welt B, zunächst streng von der ersten geschieden, ist die Welt der Information. Hier ist der Gegenpol zur Eindeutigkeit gegeben, actio non est reactio. Die Ursache erzeugt zwar eine Wirkung, aber welche aus einer Menge möglicher Wirkungen das sein wird, ist nicht vorhersehbar. Die Wirkung besitzt also gegenüber der Ursache bestimmte Freiheiten, sie ist mehrdeutig. Die Ursache beruht zwar - wie in Welt A - auf einer physischen Basis, diese ist in unserem Zusammenhang aber irrelevant. Sie hat hier ausschließlich informativen, symbolischen Charakter und führt als Wirkung zu weiteren Symbolen bzw. Handlungen.

Im vorliegenden Computerprogramm werden beide Welten simuliert und miteinander in Beziehung gesetzt, um eine bestimmte Aufgabe in Welt A unter Mitwirkung von Welt B zu lösen. Dabei wird von einem idealisierten Szenario ausgegangen, das kurz beschrieben werden soll:

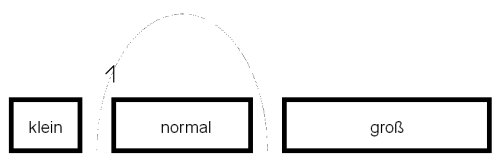
In Welt A existieren drei Hauptelemente: die "Barriere", ein "Springer" und ein "Sprecher". Springer und Sprecher erhalten ihre Namen nach der ihnen zugeordneten Hauptaktivität. Die Barriere, ein Hindernis, dessen Breite zufällig wechselt, repräsentiert die Physis, die "Natur". Die Breite des Hindernisses nimmt zufällig u unterschiedliche diskrete Werte an, wobei die einzelnen Werte mit dem Index k bezeichnet werden sollen, also k=1...u. (siehe Abb. 1).

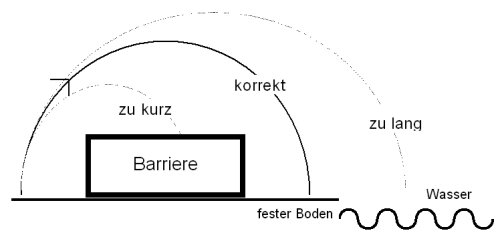
Die Aufgabe besteht darin, daß diese Barriere vom "Springer" korrekt (d.h. mit einem Sprung, der nicht zu kurz und nicht zu lang ist) übersprungen werden soll. In Abbildung 2 sind mehrere Flugbahnen des Springers eingezeichnet. Nur ein "korrekter" Sprung (durchgezogene Linie) gilt als erfolgreich, zu lange oder zu kurze Sprünge (gestrichelte Linien) werden als Mißerfolg gewertet. Die Schwierigkeit dabei ist, daß der Springer blind ist, d.h. die Breite des Hindernisses nicht selbst feststellen kann. Er ist auf Hilfe angewiesen. Sie kommt vom "Sprecher", der die jeweilige Breite des Hindernisses feststellen kann. Der Sprecher hat die Möglichkeit, Laute auszustoßen, die der Springer hören und als Grundlage für die Wahl seines Verhaltens nützen kann.

Der "blinde Springer" hat folgende Fähigkeiten:

1. Er kann "springen" (und zwar mit t vorher festliegenden Sprunglängen), aber nicht sprechen

2. Er kann "hören" (und zwar die s Sprachlaute des Sprechers), aber nicht sehen

3. Er kann das Gehörte mit bestimmter Wahrscheinlichkeit mit seiner "Entscheidung", wie weit er springt, verknüpfen.

4. Er kann den Erfolg oder Mißerfolg seines Sprunges feststellen. Erfolg erhöht die entsprechende Verknüpfungswahrscheinlichkeit zwischen gehörtem Laut und seiner Sprungweite, Mißerfolg reduziert sie.

Die Beschreibung des Zusammenhangs zwischen Hören und Springen erfolgt mittels einer Wahrscheinlichkeitsmatrix H. Sie ist eine Markoff-Matrix mit den Zeilensummen 1, also H1 = 1, die aus s Zeilen und t Spalten besteht. Ihre Elemente h(i,j), i=1...s, j=1...t, haben anfänglich alle die gleichen Werte: h(i,j) = 1/t.

Der Sprecher besitzt folgende Eigenschaften:

1. Er kann "sprechen", d.h. u unterscheidbare Laute ausstoßen, aber nicht springen

2. Er kann das Hindernis "sehen", die Breite der Barriere feststellen, aber nicht hören

3. Er kann die wahrgenommene Breite der Barriere mit bestimmter Wahrscheinlichkeit mit bestimmten Sprachlauten verknüpfen.

4. Er kann den Erfolg oder Mißerfolg des Sprunges feststellen. Erfolg erhöht die entsprechende Verknüpfungswahrscheinlichkeit zwischen wahrgenommener Barrierenbreite und geäußertem Laut, Mißerfolg reduziert sie.

Die Beschreibung des Zusammenhangs erfolgt mittels einer Wahrscheinlichkeitsmatrix G, einer Markoff-Matrix mit den Zeilensummen 1, also G1 = 1, die aus u Zeilen und s Spalten besteht. Die Elemente g(k,i), k=1...u, i=1...s, haben anfänglich alle die gleichen Werte: g(k,i) = 1/s.

Der blinde Springer agiert in Welt A, seine Hörfähigkeit ist er eine Schnittstelle zu Welt B. Der Sprecher agiert in Welt B, durch seine Beobachterrolle besitzt er eine Schnittstelle zu Welt A.

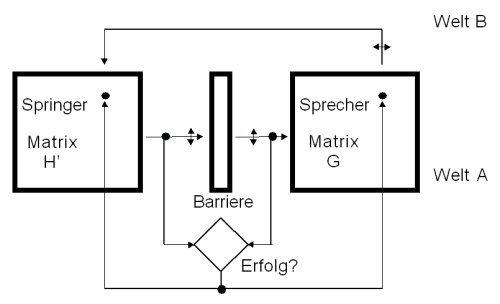
Einen Überblick über die Programmstruktur bietet Abb. 3. In der Mitte der Abbildung ist die Barriere angedeutet. Ein Zufallsgenerator wählt eine bestimmte Breite aus einer Reihe von Möglichkeiten. Der senkrechte Doppelpfeil symbolisiert die Variabilität der Barriere. Rechts von der Barriere ist die Sprecher-Matrix in Form eines Rechtecks dargestellt. Das Rechteck soll die Übergangsmatrix verkörpern, die eine spezielle beobachtete Breite des Hindernisses (Zeileninput) mit einem Laut verknüpft, der zufällig ausgewählt wird (Spaltenoutput, als variabel dargestellt durch den waagrechten Doppelpfeil). Der blinde Springer (Rechteck auf der linken Seite der Graphik) "hört" den Laut (Zeileninput von H) und verknüpft ihn zufällig mit einer Sprungweite (Spaltenoutput von H). In Abb. 3 ist die Matrix H gestürzt dargestellt (Spalten und Zeilen vertauscht gegenüber der traditionellen Konvention, daß die Zeilen horizontal verlaufen).

Die Schwierigkeit besteht darin, daß der Beobachter zwar etwas sagen kann, aber die Bedeutung des Gesagten anfänglich noch nicht festliegt. Er "stammelt" also zunächst nur einen Laut. Der Springer kann den Laut hören und dann springen, und zwar entweder kürzer, oder länger als die Barriere, oder korrekt. Ein Vergleich zwischen Barrierenbreite und tatsächlichem Sprung wird als Erfolg bzw. Mißerfolg verbucht (siehe auch Abb. 2). Das korrekte Springen bedeutet Erfolg, das nichtkorrekte einen Mißerfolg. Erfolg bzw. Mißerfolg verändern die Kopplungswahrscheinlichkeiten der Übergangsmatrizen bei Sprecher und Springer.

Die Realisierung des Simulationsmodells

Das Programm wurde mit einer graphischen Oberfläche versehen (siehe Abb. 4), auf der sich Sprecher und Springer befinden. Der Springer setzt mit einer Wurfparabel über die Barriere hinweg, bzw. er springt zu weit (ins Wasser) oder zu kurz (auf die Spitzen der Barriere).

Für die Barrierenbreiten wählten wir u = 3, die möglichen Breiten werden mit KLEIN, NORMAL und GROSS bezeichnet. Die Sprungweite des Springers umfaßt t = 4 Möglichkeiten, ZUKURZ, KURZ, MITTEL und LANG. u und t sind nicht unbedingt gleich. t ist in unserem Beispiel um 1 größer als u, da der Springer nach unseren Annahmen auch noch kürzer als die kürzeste mögliche Barriere springen kann. Die s = 3 Sprachlaute symbolisierten wir mit A, B und C, obwohl die Wahl der Laute völlig beliebig ist.

Formal läßt sich der Ablauf der Simulation wie folgt darstellen:

Ein Zufallsgenerator bestimmt zunächst die Barrierenbreite k*, die der Sprecher feststellt (z.B. k* = 2; NORMAL). Zur Bestimmung des Sprachlauts zieht ein zweiter Zufallsgenerator eine Zahl y*, 0 ² y* < 1, die zunächst einer Gleichverteilung entnommen wird, da die g(k,i) noch alle gleich groß sind. Das zu y* gehörige i*, das den Sprachlaut festlegt, wird aus folgender Beziehung bestimmt:

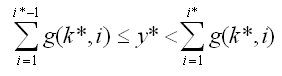
Für diese und die nächste Formel soll folgende Konvention gelten: Ist der letzte Wert des Laufindex der Summation kleiner als der erste, also z.B. 0 (der letzte Wert) < 1 (der erste Wert), so wird gar keine Summation durchgeführt. Das Ergebnis der linken Seite wäre in diesem Fall 0. Ferner soll für i* = s bzw. für j* = t auf der rechten Seite das "kleiner gleich" Zeichen anstelle des "kleiner" Zeichens stehen. Z.B. sei y*=0.13426556, damit wird i* = 1, als Sprachlaut also "A" ausgewählt. Der Sprecher sagt "A" zum Springer.

Beim Springer spielt sich ein analoger Vorgang ab. Er "wählt" auf Basis einer gleichverteilten Zufallszahl z* unter der Bedingung des gehörten Sprachlauts (im Beispiel: i*=1; Sprachlaut "A") seine Sprungweite j* aufgrund der Beziehung

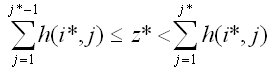
Z.B. sei z*=0,936274, damit wird j* = 4, als Sprungweite also "LANG" ausgewählt. Der Springer springt, aber zu weit, daher, wie beide feststellen, ein Mißerfolg.

Nun wird gelernt, d.h., die Wahrscheinlichkeiten g und h werden verändert. Da ein Mißerfolg vorliegt, wird

gesetzt, ebenso

Faktorg und Faktorh sind die Lernparameter, Faktorg > 1 und Faktorh > 1. In unserem Beispiel wählten wir Faktorg = Faktorh = 2, also

gesetzt, ebenso

Alle anderen Elemente der Markoff-Matrizen bleiben unverändert.

Im Falle eines Erfolgs wären die Wahrscheinlichkeiten vergrößert worden:

und

Nun ist aber die Zeilensummenbedingung der Markoff-Matrix verletzt. Eine Normierung auf Zeilensumme = 1 behebt dieses Problem. Es gilt also zusätzlich

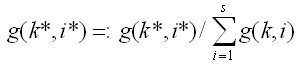und

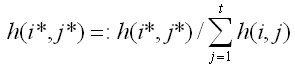
Das Ergebnis

Wenn in einer Iteration der Simulation ein korrekter (nicht korrekter) Sprung erfolgte, werden die dazugehörigen Elemente der beiden Markoff-Matrizen (also je eines pro Matrix) vergrößert (verkleinert), alle anderen wegen der Normierungserfordernis verkleinert (vergrößert). Die so entstandenen Zeilenmaxima bzw. -minima können während der Anfangsphase eines Simulationslaufes durchaus noch ihren Platz ändern. Nach einigen -zig Versuchen "lernt" der Springer jedoch, auf den speziellen Zuruf des Sprechers korrekt zu springen, der Sprecher "lernt", die jeweilige Barrierenbreite mit einem jeweils dazugehörigen Sprachlaut zu bezeichnen, der sich im Lauf der Zeit nicht mehr ändert. Die entsprechenden Wahrscheinlichkeiten konvergieren gegen 1 (bzw. 0). Die anfänglich flexible "Wortwahl" ist starr und irreversibel geworden. Die Worte besitzen eine für die weitere Simulation unveränderliche Bedeutung.