Formelsammlung: Rechenregeln

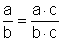
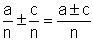
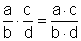
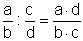
Grundlegende Rechengesetze

Kommutativgesetz der Addition:

a + b = b + a
Assoziativgesetz der Addition:

(a + b) + c = a + (b + c)
Kommutativgesetz der Multiplikation:

a·b = b·a
Assoziativgesetz der Multiplikation:

(a·b)·c = a·(b·c)
Distributivgesetz:

a·(b + c) = a·b + a·c

Rechnen mit negativen Zahlen

+(+a) = +a
+(-a) = -a
-(+a) = -a
-(-a) = +a

(+a)·(+b) = +ab
(+a)·(-b) = -ab
(-a)·(+b) = -ab
(-a)·(-b) = +ab

Rechnen mit Brüchen

Erweitern / Kürzen:

Addition / Subtraktion:

Multiplikation.

Division:

Potenzen von Binomen

(a + b)² = a² + 2ab + b²

(a - b)² = a² - 2ab + b²

(a + b)³ = a³ + 3a²b + 3ab² + b³

(a - b)³ = a³ - 3a²b + 3ab² - b³

Zerlegung von Binomen

a² - b² = (a - b)(a + b)

a² + b² kann nicht zerlegt werden!

a³ - b³ = (a - b)(a² + ab + b²)

a³ + b³ = (a + b)(a² - ab + b²)

Zurück