(Betriebs-) Kostenfunktion

K(x)

Fixkosten

K_F = K(0)

variable Kosten

K_var = K(x) - K_F

Grenzkosten

K’(x)

degressive Kosten

K''(x) < 0

progressive Kosten

K''(x) > 0

Kostenkehre
(Minimum der Grenzkosten)

K''(x) = 0

Stückkostenfunktion

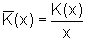
Betriebsoptimum
(Minimum der Stückkosten)

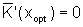oder

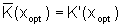
LPU (langfristige Preisuntergrenze)

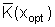
variable Stückkosten

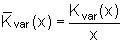
Betriebsminimum
(Minimum der variablen Stückkosten)

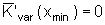oder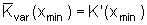

KPU (kurzfristige Preisuntergrenze)

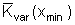
Nachfragefunktion (Preisfunktion)

p(x)

Höchstpreis (Maximalpreis, Prohibitivpreis)

p(0)

Sättigungsmenge

p(x_s) = 0

Erlösfunktion (Umsatzfunktion)

E(x) = p·x bzw. p(x)·x

Gewinnfunktion (Erfolgsfunktion)

G(x) = E(x) - K(x)

Gewinngrenzen
(bzw. Gewinnschwelle und -grenze)

G(x) = 0

gewinnmaximierende Menge
(Cournot'sche Menge)

G’(x_c) = 0

Cournot'scher Punkt

C( x_c / p(x_c) )