Nr. 10 / September 2005
Hallo! Ich hoffe, ihr habt die Ferien gut verbracht und seid frisch und ausgeruht für das neue Arbeitsjahr. Ich werde ab jetzt versuchen, alle zwei Monate einen Newsletter zu schreiben. Das heutige Thema soll noch ein bisschen an die Reisezeit erinnern:

Zuerst ein Rätsel:
Drei Flugzeuge fliegen von Wien weg. Das erste fliegt immer nach Westen, das zweite nach Norden und das dritte nach Nordwesten. Wo werden sie ankommen?
Die Antwort lautet: Das erste Flugzeug fliegt entlang eines Breitenkreises um die Erde und kommt wieder nach Wien zurück. Das zweite gelangt bis zum Nordpol - von dort geht es nicht mehr weiter nach Norden. Und das dritte Flugzeug fliegt ebenfalls zum Nordpol, aber nicht auf dem direkten Weg, sondern auf einer spiralförmigen Bahn.
Um solche und ähnliche Aufgaben zu lösen, braucht man möglichst genaue Weltkarten. Das Problem dabei ist, die annähernd kugelförmige Erdoberfläche auf eine ebene Karte abzubilden. Wir werden sehen, dass es dafür verschiedene Möglichkeiten gibt, die alle ihre Vor- und Nachteile haben.
Grundbegriffe
Wir nehmen der Einfachheit halber an, dass die Erde eine Kugel ist. Jeder Punkt auf der Erdoberfläche ist durch seine geographische Breite β und seine geographische Länge λ festgelegt.
Der kürzeste Weg zwischen zwei Punkten auf der Erdoberfläche verläuft entlang eines Großkreises. Das ist der größte Kreis, den man auf einer Kugel zeichnen kann. Die Meridiane und der Äquator sind Großkreise, die anderen Breitenkreise nicht. (Das erste Flugzeug aus dem Rätsel muss ständig eine leichte Rechtskurve fliegen.) Der Unterschied kann beträchtlich sein. So liegen z.B. Tokio und San Francisco beide auf ca. 37° nördlicher Breite. Der kürzeste Weg zwischen den beiden Städten verläuft aber, wie man auf einem Globus sieht, nahe dem nördlichen Rand des Pazifik. Er ist um ca. 500 km kürzer als die Strecke entlang des 37. Breitengrads. Einen solchen Weg bezechnet man als Orthodrome.
Für die Schiffahrt ist eine andere Art von Kurven wichtig: die Loxodrome, die jeden Meridian unter dem selben Winkel schneidet. (Das dritte Flugzeug aus dem Rätsel beschreibt eine Loxodrome.) Es ist für den Steuermann einfacher, entlang einer Loxodrome zu fahren, weil er dabei immer denselben Kurs einhalten kann.
Die "ideale" Karte
An eine ideale Weltkarte würden wir folgende Forderungen stellen:
Längentreue: alle Strecken sollen im gleichen Maßstab abgebildet werden
Winkeltreue: alle Winkel sollen in ihrer wahren Größe erscheinen
Flächentreue: die Verhältnisse zwischen Flächen sollen richtig dargestellt werden
Leider hat man im 19. Jahrhundert mit Hilfe der Differentialgeometrie gezeigt, dass keine Karte alle drei Forderungen erfüllen kann. Es ist nicht einmal möglich, dass sie in alle Richtungen längentreu ist. Man kann eben eine Kugeloberfläche nicht auf eine Ebene abbilden, ohne dass sie dabei verzerrt wird. Man muss also Kompromisse schließen und die Projektion auswählen, die für einen bestimmten Zweck am besten geeignet ist.
Einige historische Bemerkungen
Den ersten Weltkarten kam es noch nicht auf Genauigkeit an, sondern eher auf eine schematische Darstellung. Ein berühmtes Beispiel ist die "Tabula Peutingeriana", eine Karte des römischen Straßennetzes. (Eine kopie aus dem 11. Jahrhundert befindet sich in der Österreichischen Nationalbibliothek.) Hier ist ein Ausschnitt zu sehen - am oberen Rand erkennt man Vindobona (Wien) und Carnuntum, in der unteren Hälfte das adriatische Meer. Es kommt hier nur auf den ungefähren Verlauf der Straßen an, etwa so wie bei einer modernen Darstellung der Wiener U-Bahn-Linien.
Die mittelalterlichen Weltkarten sind nach einem bestimmten philosophisch-theologischen Schema gezeichnet: in der Mitte der Welt liegt Jerusalem, darum sind die Erdteile Europa, Asien und Afrika angeordnet, getrennt durch das Mittelmeer. Das kreisförmig dargestellte Ozean umschließt das alles. Ein besonders schönes Beispiel ist die Ebstorfer Weltkarte. Man kann aus solchen Karten aber nicht schließen, dass die Menschen im Mittelalter die Erde für flach hielten. Die Kugelform der Erde war damals schon selbstverständlich, aber wie sollte eine Karte anders aussehen als flach?
Die ersten Überlegungen zu einer einigermaßen genauen Darstellung der (damals bekannten)
Welt stammen vom Astronomen Klaudios Ptolemaios (ca. 100 - 160), bekannt vor allem
durch das "ptolemäische Weltbild" (die Vorstellung, dass die Erde im Mittelpunkt des
Universums steht). Ptolemaios stellte den Breitenkreis durch Rhodos als Kreisbogen dar,
auf dem er die Entfernungen maßstabgetreu einzeichnete. Die Meridiane stellte er als
Geraden dar, die von einem Punkte ausgingen - es handelt sich also um eine Art Kegelprojektion
(siehe unten). Südlich des Äquators ließ er sie wieder zusammenlaufen (siehe
hier,
zweites Bild).
Mit dieser Darstellung war Ptolemaios noch nicht ganz zufrieden, weil die Meridiane
am Äquator abgeknickt waren. Er entwickelte daher noch eine andere Karte, bei der drei
Breitenkreise (durch Thule im hohen Norden, Syene in Ägypten und einer südlich des
Äquators) längentreu abgebildet wurden. Dadurch waren auf jedem Meridian drei Punkte
vorgegeben, die er durch einen Kreisbogen verband (siehe
hier,
erstes Bild).
Im 16. Jahrhundert, dem Zeitalter der großen Entdeckungen, wurde die Frage nach Weltkarten wieder aktuell. Damals wurden die Vorschläge des Ptolemaios aufgegriffen und Karten nach ihnen gedruckt. Eine andere Darstellung stammt vom Wiener Hofastronomen Johann Stöberer, genannt Stabius. Er stellte einen Meridian längentreu als Gerade dar. Die Breitenkreise trug er, ebenfalls längentreu, auf Kreisbögen um den Nordpol auf. So erhielt er eine hübsche herzförmige Karte, die sogar flächentreu ist.
1568 stellte der flämische Kartograph Gerhard Kremer, genannt Mercator, die nach ihm benannte Weltkarte fertig, die für die Schiffahrt von größter Bedeutung wurde. Mit ihr werden wir uns weiter unten noch beschäftigen. Er stellte auch die ersten Globen her.
Im 18. Jahrhundert beschäftigten sich einige Mathematiker mit theoretischen Fragen zu Kartenprojektionen. (Dieses Thema gehört in das Gebiet der Differentialgeometrie.) Johann Heinrich Lambert, ein Autodidakt, veröffentlichte 1772 ein Werk, in dem er einige neue Darstellungen einführte. Die meisten von ihnen sind bis heute in Verwendung.
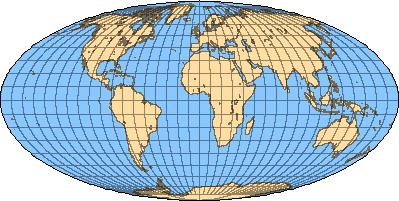
Es gibt noch unzählige andere Typen von Karten - die elliptische Darstellung am Anfang des Artikels wurde 1805 von Karl Mollweide vorgeschlagen.
Projektion auf eine Ebene: azimutale (planare) Karten
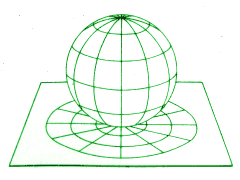
Stellen wir uns vor, wir haben ein Drahtmodell von einem Globus, das das Gradnetz und die Erdteile zeigt, und eine Lampe. Wenn wir jetzt den Globus an einem Punkt, z.B. dem Nordpol, an eine Ebene halten, wird das Gradnetz auf diese Ebene projiziert. Aus diesem Grund spricht man von einer Projektion. Die Meridiane werden auf Geraden durch den Pol abgebildet, die Breitenkreise auf konzentrische Kreise. Der Azimut - der Winkel zwischen zwei Meridianen - erscheint bei dieser Art von Projektion in wahrer Größe. (Natürlich kann man auch jeden anderen Punkt als Zentrum wählen. Für den Nordpol kann man sich aber die Verhältnisse am besten vorstellen.)
|
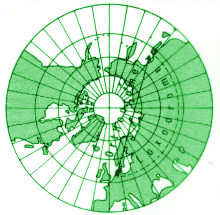
Wenn die Lampe sich im Mittelpunkt des Globus befindet, erhalten wir eine zentrale oder gnomonische Projektion. Sie hat den Vorteil, dass Großkreise als Geraden abgebildet werden. Man kann also leicht den kürzesten Weg zwischen zwei Punkten einzeichnen. Allerdings werden Gebiete, die weiter vom Pol entfernt liegen, sehr stark verzerrt. (Der Äquator kann überhaupt nicht mehr dargestellt werden.) In der Praxis projiziert man natürlich nicht einen Globus an die Wand, sondern berechnet die Position der einzelnen Punkte. Ein Ort mit der geographischen Breite β hat vom Nordpol den Winkelabstand φ = π/4 - β (wir geben Winkel im Bogenmaß an); auf der Karte beträgt dieser Abstand, wobei wir den Kugelradius als Einheit nehmen: r = tan φ |
 |
|
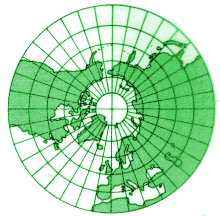
Die Verzerrung wird nicht ganz so groß, wenn wir die Lampe in den Südpol legen. Wir erhalten dann eine stereographische Projektion. Sie ist winkeltreu, und Kreise werden als Kreise dargestellt. Daher wird diese Projektion für topographische Karten verwendet. Der Abstand eines Punktes vom Pol ist r = 2·tan(φ/2) (Ptolemaios benutzte diese Projektion schon für Sternkarten, aber er kam noch nicht auf die Idee, dass man sie auch für eine Karte der Erde verwenden könnte.) |
 |
|
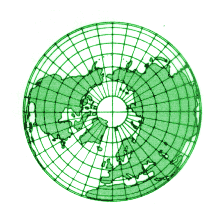
Wenn die Lichtstrahlen normal zur Projektionsebene einfallen (wir können uns vorstellen, dass die Lichtquelle sehr weit entfernt ist), erhalten wir eine orthografische Projektion. Sie zeigt die Erde so, wie sie aus dem Weltraum aussehen würde. Die Abbildungsgleichung lautet r = sin φ |
 |
|
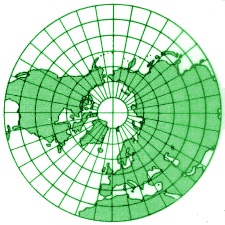
Am einfachsten ist es, wenn wir die Meridiane in ihrer wahren Länge einzeichnen. Das ist eigentlich keine Projektion im strengen Sinn mehr. Wir erhalten so eine Karte, die auf den Meridianen längentreu ist - man bezeichnet sie als mittelabstandstreue bzw. speichentreue Karte. Die Abbildungsgleichung ist besonders einfach: r = φ |
 |
|
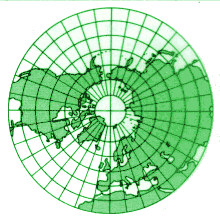
Trägt man nicht die Länge der Kreisbögen, sondern der entsprechenden Sehnen ab (sozusagen auf direktem Weg durch die Erde gemessen), erhält man Lamberts Azimutalkarte, eine flächentreue Abbildung. Die Gleichung lautet r = 2·sin(φ/2) |
 |
Zylinderprojektionen
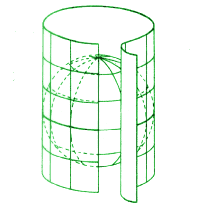
Wir können auch eine Karte herstellen, indem wir ein Blatt Papier in Form eines Zylinders um den Globus wickeln, die Karte übertragen und das Blatt wieder abwickeln. Eine solche Darstellung eignet sich besonders gut, wenn man die Gebiete in der Nähe des Äquators darstellen will. Der Zylinder kann die Kugel aber auch entlang eines beliebigen Großkreises berühren.
|
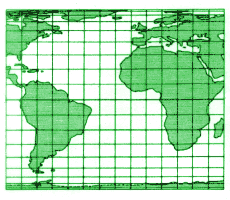
Bei Lamberts Zylinderprojektion sind die Projektionsstrahlen waagrecht (also normal auf die Zylinderfläche). Die Gebiete, die weiter vom Äquater entfernt liegen, werden zwar der Breite nach auseinandergezogen, aber der Länge nach um denselben Faktor verkürzt. Daher ist diese Darstellung flächentreu. Wenn wir die Bilder von Äquator und Nullmeridian als Koordinatenachsen auffassen, hat ein Ort mit der geograohischen Breite β und Länge λ auf der Karte die Koordinaten x = λ, y = sin β Wenn man will, dass die gemäßigten Breiten nicht so stark verzerrt werden, kann man einen schmaleren Zylinder als Projektionsfläche wählen, z.B. einen, der den Globus am 45. Breitenkreis (nördlich und südlich) schneidet. Dann wird einfach die Kartenbreite um den Faktor 0,7 verkürzt. |
 |
|
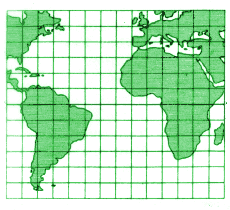
Am einfachsten ist es, wenn man die geographische Breite vom Äquator aus nach oben bzw. unten aufträgt. Die Maschen des Gradnetzes erscheinen dann als Quadrate; man bezeichnet eine soclhe Karte daher als quadratische Plattkarte. Sie ist auf dem Äquator und den Meridianen längentreu. Die Abbildungsgleichungen lauten einfach x = λ, y = β Auch hier kann man die Breite verkürzen, dann erhält man eine rechteckige Plattkarte. |
 |
|
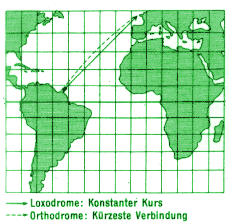
Die Mercatorkarte ist eine winkeltreue Darstellung. Die Loxodromen (Wege mit konstantem Kurswinkel, s.o.) erscheinen auf ihr als Geraden. Deshalb war diese Karte besonders wichtig für die Schiffahrt. Ein Nachteil der Mercatorkarte besteht darin, dass die weiter vom Äquator entfernten Gebiete extrem verzerrt werden. So erscheint z.B. Grönland genauso groß wie Afrika. Die Pole können überhaupt nicht mehr dargestellt werden. Die Abbildungsgleichungen lauten x = λ, y = ln(tan(β/2 + π/4)) Diese eher komplizierte Gleichung erhält man durch Integrieren. Man weiß nicht genau, wie Mercator seine Karte konstruiert hat, denn er lebte ca. 100 Jahre vor der Erfindung der Differential- und Integralrechnung! |
 |
Kegelprojektionen
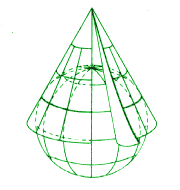
Wenn man die gemäßigten Breiten auf einer Karte darstellen will (z.B. Gebiete zwischen 30° und 60° nördlicher Breite), kann man dals Projektionsfläche auch einen Kegel benutzen, der Globus entlang eines Breitenkreises berührt. Auch hier gibt es flächen-, längen- und winkeltreue Projektionen.
Zu diesem Thema gäbe es natürlich noch viel mehr zu sagen. Auf http://eddy.uni-duisburg.de/Treitz/Erdkarten.htm/start.htm, der Homepage von Prof. Norbert Treitz, kann man viele Bilder bewundern - die Kommentare sind allerdings etwas knapp. Ausführliche Erklärungen auf Englisch finden sich auf http://www.progonos.com/furuti/MapProj/CartIndex/cartIndex.html.
Viel Spaß bis zum nächsten Mal!
Jutta
E-mail: gut.jutta.gerhard@chello.at