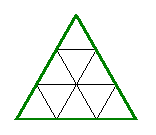
3 · 3 = 9
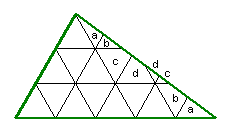
5 · 3 = 15
(die Flächen mit denselben Buchstaben
ergeben zusammen jeweils ein G-Dreieck)
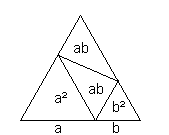
(a + b)² = a² + 2ab + b²
Nr. 18 / April 2007
Wie vor kurzem bekannt wurde, haben Forscher eine bisher kaum bekannte Volksgruppe in Tryan Gully (Zentralasien) untersucht. Dieses Volk war von der übrigen Welt fast völlig abgeschieden und hat eine ganz eigene Geometrie entwickelt. Ihre Grundlage ist nicht, wie in der klassischen Geometrie, das Quadrat, sondern das gleichseitige Dreieck (ab jetzt G-Dreieck genannt). Und der wichtigste Winkel ist nicht der rechte Winkel, sondern 60°, der Innenwinkel des gleichseitigen Dreiecks. Er wird "gerechter Winkel" genannt, weil in diesem Dreieck alle drei Winkel gerecht verteilt sind. Auch der "doppelt-gerechte Winkel" von 120° tritt häufig auf.
Die Häuser der Tryangullianer bestehen meist aus dreieckigen und sechseckigen Räumen. Die Wände sind zwar senkrecht (aus naheliegenden Gründen), aber sie werden innen oft mit schräg gespannten Tüchern verdeckt. Die Forscher sind der Ansicht, dass das eine Erinnerung an die Nomadenvergangenheit der Bewohner darstellt - die Wohnungen sind einem Zelt nachgebildet. Auch die Felder haben Dreieck- oder Sechseckform.
Die gebräuchlichste Längeneinheit ist das Fuß, und die Flächeneinheit ist das Dreiecksfuß - die Fläche eines G-Dreiecks mit 1 Fuß Seitenlänge. Die Arithmetik ist genauso aufgebaut wie die unsere, aber die geometrischen Vorstellungen dahinter sind anders: Das Produkt zweier Zahlen a und b ist der Flächeninhalt des "gerechtwinkeligen" Dreiecks, also eines Dreiecks mit einem Winkel von 60°, der von den Seiten a und b eingeschlossen wird. Das "Dreieck" einer Zahl a (entspricht unserem a²) ist der Flächeninhalt eines G-Dreiecks mit der Seitenlänge a. Die "Dreieckswurzel" aus e ist die Seitenlänge eines G-Dreiecks mit dem Flächeninhalt e. Weil die Flächen in Dreiecksfuß gemessen werden, ergeben sich dabei genau die selben Rechenregeln wie in der klassischen Mathematik. Sätze wie die bekannte binomische Formel
(a + b)² = a² + 2ab + b²
gelten in der tryangullianischen Mathematik genauso wie in der unseren.
|
3 · 3 = 9 |
5 · 3 = 15 |
(a + b)² = a² + 2ab + b² |
Flächen von Vierecken sind natürlich etwas komplizierter zu berechnen. Ein Quadrat der Seitenlänge 1 hat den Flächeninhalt 4/√3 ~ 2,3094. Die Fläche des Einheitskreises beträgt ca. 7,2552. Diese Zahl spielt in der tryangullianischen Mathematik eine ähnliche Rolle wie π für uns.
Rauminhalte werden in "Tetra-Fuß" gemessen - dem Volumen eines Tetraeders mit 1 Fuß Seitenlänge. In der Praxis erweist sich das aber als ziemlich mühsam. Deswegen haben die Tryangullianer auch keine ausführliche Geometrie des Raumes entwickelt.
Für geometrische Konstruktionen verwenden die Tryangullianer G-Dreiecke aus Holz, es gibt aber auch die auch bei uns bekannten Zeichendreiecke mit den Winkeln 30°, 60° und 90° (also ein halbes G-Dreieck). Diese Figur betrachtete auch Plato als das schönste Dreieck - eine interessante kulturgeschichtliche Parallele.
Einer der bedeutendsten tryangullianischen Mathematiker war Pitt A. Goras. Er untersuchte "gerechtwinkelige" Dreiecke und fand dabei den nach ihm benannten Lehrsatz:
Errichtet man über den Seiten eines gerechtwinkeligen Dreiecks G-Dreiecke, so ist die Summe der Dreiecke über den Seiten, die den gerechten Winkel einschließen, gleich dem Dreieck über der dritten Seite, vermehrt um das ursprüngliche Dreieck.
In unserer Schreibweise bedeutet das:
Wenn in einem Dreieck der Winkel γ = 60° beträgt, so ist
a² + b² = c² + ab.
Wer sich ein bisschen mit Trigonometrie auskennt, wird in dieser Formel den Cosinussatz erkennen (c² = a² + b² - 2ab cos(60°) = a² + b² - ab, weil cos(60°) = ½). Goras gab aber einen rein geometrischen Beweis (hier übersetzt in unsere Schreibweise):
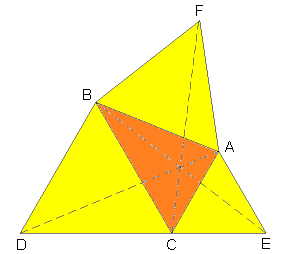
Das Dreieck ABC hat bei C einen Winkel von 60°. Es ist zu zeigen: Fläche(BCD) + Fläche(ACE) = Fläche(ABF) + Fläche(ABC).
BD ist parallel zu AC, also ist das Dreieck BCD flächengleich zum Dreieck BAD. Dieses Dreieck geht durch eine Drehung um 60° in das Dreieck BFC über. Die Dreiecke BCD und BCF haben also den gleichen Flächeninhalt. Genauso zeigt man, dass die Dreiecke ACE und ACF den gleichen Flächeninhalt haben. Also sind die Dreiecke BCD und ACE zusammen genauso groß wie das Viereck AFBC, was zu beweisen war.
Der zweite Satz von Goras bezieht sich auf "doppelt-gerechtwinkelige" Dreiecke:
Errichtet man über den Seiten eines doppelt-gerechtwinkeligen Dreiecks G-Dreiecke, so ist die Summe der Dreiecke über den Seiten, die den doppelt-gerechten Winkel einschließen, gleich dem Dreieck über der dritten Seite, vermindert um das ursprüngliche Dreieck.
In unserer Schreibweise:
Wenn in einem Dreieck der Winkel γ = 120° beträgt, so ist
a² + b² = c² - ab.
Der Beweis erfolgt so ähnlich wie der vorige.
Pitt A. Goras interessierte sich auch dafür, bei welchen "gerechtwinkeligen" Dreiecken alle Seitenlängen ganze Zahlen sind. Er fand dafür eine einfache Formel: Wenn man für p und q beliebige natürliche Zahlen mit p > 2q einsetzt, sind
a = p² - q²
b = 2pq - q²
c = p² - pq + q²
die Seiten eines "gerechtwinkeligen" Dreiecks. Eine weitere interessante Eigenschaft dieser Dreiecke ist folgende: Ersetzt man b durch a - b, so erhält man ein neues "gerechtwinkeliges" Dreieck, das man mit dem ursprünglichen zu einem G-Dreieck zusammensetzen kann. Goras nannte solche Paare "komplementäre Dreiecke".
In der nachfolgenden Tabelle sind einige solche "goräischen" Dreiecke zusammengestellt:
p
q
Dreieck (a, b, c)
komplementäres Dreieck
2
1
(3, 3, 3)
-
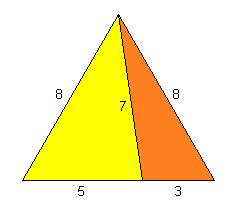
3
1
(8, 5, 7)
(8, 3, 7)
4
1
(15, 7, 13)
(15, 8, 13)
5
2
(21, 16, 19)
(21, 5, 19)
6
1
(35, 11, 31)
(35, 24, 31)
7
1
(48, 13, 43)
(48, 35, 43)
7
3
(40, 33, 37)
(40, 7, 37)
Einige Kombinationen habe ich ausgelassen, weil sie nur Vielfache von schon gefundenen Dreiecken ergeben. Weitere Zahlentripel findet ihr auf http://www.jimloy.com:80/puzz/3triangl.htm.
Ersetzt man a durch a - b (das heißt, man schneidet von dem Dreieck ein G-Dreieck mit der Seitenlänge b ab), so erhält man ein "doppelt-gerechtwinkeliges" Dreieck. Die Bildungsvorschrift für "doppelt-gerechtwinkelige" Dreiecke mit ganzzahligen Seitenlängen lautet daher:
a = p² - 2pq
b = 2pq - q²
c = p² - pq + q²
Die tryangullianische Kultur und Mathematik soll weiter erforscht werden - sicher gibt es dabei noch viele interessante Erkenntnisse. Ich freue mich über alle Anregungen!
Jutta
P.S.: Die "Geometrie von Tryan Gully" war eigentlich als Aprilscherz gedacht. Inzwischen habe ich herausgefunden, dass der amerikanische Architekt und Philosoph Richard Buckminster Fuller (1895 - 1983) auch ein solches Konzept entwickelt hat. Seiner Meinung nach ist ein System, das auf 60°-Winkeln aufbaut, natürlicher als unser rechtwinkeliges System, weil diese Winkel in den dichtesten Kugelpackungen vorkommen. In seinem Buch "Synergetics" (1975) schreibt er unter anderem:
"200.01 Synergetics is a triangular and tetrahedral system. It uses 60-degree-coordination instead of 90-degree-coordination...
205.04 The metaphysically permitted frame of reference for all the asymmetrical physical experience of humanity is characterized by the 60-degree-coordination with which synergetics explores nature's behaviors - metaphysical or physical.
206.00 ... The unit of modular volumetric measurement is the tetrahedron, whose 60-degree-angles and six equilength edges disclose omnipersistent, one-to-one correspondence of radial wave modular growth with circumferential modular frequency growth of the totally involved vectorial geometry. This means that angular and linear accelerations are identical. This is a rational convenience prohibited by 90-degree-coordination, whose most economical circumferential geometries are in most cases inherently irrational."
Leider sind die Texte nur schwer zu übersetzen, weil Buckminster Fuller seine eigene Terminologie entwickelt hat. Wie im Zitat erwähnt, benutzt er als Einheit des Volumens das Tetraeder mit Einheitslänge. Das Volumen des Oktaeders beträgt dann 4 Einheiten, das des Würfels, der dem Tetraeder umschrieben werden kann, 3 Einheiten und der Rauminhalt des Kuboktaeders (der bei Buckminster Fuller "vector equilibrum" heißt) 20 Einheiten. "Bucky" hat dieses Konzept konsequent durchgezogen - allerdings finde ich es ziemlich gewöhnungsbedürftig.
Auf http://www.rwgrayprojects.com/synergetics/synergetics.html kann man das ganze Werk online lesen, und auf http://www.grunch.net/synergetics/intro.html gibt es einige Erklärungen.
E-mail: gut.jutta.gerhard@chello.at