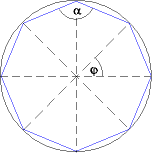
Der Mittelpunktswinkel φ in einem regelmäßigen n-Eck beträgt 360°/n.
Daher ist der Innenwinkel α bei einem Eckpunkt 180° - 360°/n.
Beim Achteck ist z.B. φ = 360°/8 = 45° und
α = 180° - 45° = 135°.Nr. 4 / Dezember 2004
Zwei Nachträge zur letzten Nummer:
Bei der Goldbachschen Vermutung sollte es heißen: "... seiner Meinung nach könnte jede gerade Zahl größer oder gleich 4 als Summe von zwei Primzahlen dargestellt werden."
Und was die Fermatschen Primzahlen betrifft: Man hat schon von viel mehr Fermatzahlen bewiesen, dass sie zusammengesetzt sind (alle von F5 bis F32 und noch einige darüber hinaus), aber nur von F5 bis F11 kennt man alle Faktoren.
Diesmal will ich mich mit einem Thema aus der Geometrie befassen, nämlich mit Polygonen bzw. Vielecken. Es gibt viele Dreiecke, Vierecke usw., aber am symmetrischsten sind die regelmäßigen Polygone. Bei ihnen sind alle Seiten gleich lang und alle Winkel gleich groß. Sie können einem Kreis eingeschrieben oder umschrieben werden.
Der Mittelpunktswinkel φ in einem regelmäßigen n-Eck beträgt 360°/n.
Daher ist der Innenwinkel α bei einem Eckpunkt 180° - 360°/n.
Beim Achteck ist z.B. φ = 360°/8 = 45° und
α = 180° - 45° = 135°.
Schon die griechischen Mathematiker haben sich gefragt, welche regelmäßigen Vielecke mit Zirkel und Lineal konstruiert werden können. Genauer gesagt: Wir haben einen Kreis gegeben und wollen diesem ein regelmäßiges n-Eck einschreiben. Am einfachsten erhält man das regelmäßige Sechseck: man schlägt den Kreisradius auf dem Umfang ab. Wenn man jeden zweiten Eckpunkt auslässt, erhält man ein gleichseitiges Dreieck. Und auch ein Quadrat kann einfach konstruiert werden, indem man zwei aufeinander normale Durchmesser einzeichnet.
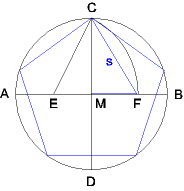Auch ein regelmäßiges Fünfeck kann mit Zirkel und Lineal konstruiert werden:
In einem Kreis mit dem Mittelpunkt M zeichnen wir zwei aufeinander normale Kreisdurchmesser
AB und CD. Dann konstruieren wir E, den Mittelpunkt von MA, stechen dort mit dem Zirkel
ein und zeichnen einen Kreisbogen mit Radius EC. Der Schnittpunkt mit dem Durchmesser ist F.
Dann ist die Strecke CF die Seite des regelmäßigen Fünfecks, das man dem Kreis
einschreiben kann (und MF die Seite des regelmäßigen Zehnecks).
Wenn man Dreieck und Fünfeck kombiniert, kann man das regelmäßige 15-eck konstruieren. Außerdem kann man in jedem Polygon den Mittelpunktwinkel halbieren und so die Seiten verdoppeln. Daher kann man auch regelmäßige Vielecke mit 8, 10, 12, ... Ecken konstruieren.
Viele Jahrhunderte dachte man, dass das alle Möglichkeiten wären. Doch 1798 machte der junge Carl Friedrich Gauss (1777 - 1855) eine aufregende Entdeckung: Er fand heraus, dass man ein regelmäßiges n-Eck mit Zirkel und Lineal konstruieren kann, wenn n eine Fermatsche Primzahl, also eine Primzahl der Form 22k + 1 ist (siehe Mathe-Newsletter 3). Daher sind auch das regelmäßige 17-, 257- und 65537-eck konstruierbar.
Mit regelmäßigen Polygonen kann man die ganze Ebene bedecken, wie eine Wand mit Kacheln. Bei einer regulären Kachelung (englisch: tesselation) sind alle Kacheln gleich. Das geht nur, wenn der Innenwinkel α ein Teiler von 360° ist. Dafür gibt es nur drei Möglichkeiten: An einer Ecke können je 6 gleichseitige Dreiecke, 4 Quadrate oder 3 regelmäßige Sechsecke aneinanderstoßen. Diese Kachelungen bezeichnen wir mit den Abkürzungen 36, 44 bzw. 63. (Die erste Zahl gibt also immer den Typ der Kachel an, die zweite die Anzahl, die um eine Ecke herum liegen.)
Wenn man die Mittelpunkte der Kacheln miteinander verbindet, erhält man sogenannte duale Kachelungen - die Flächen der einen Kachelung entsprechen den Ecken der anderen und umgekehrt. Aus 36 wird 63, 44 ist zu sich selbst dual.
Eine halbreguläre Kachelung besteht aus verschiedenen Polygonen, aber an jeder Ecke stoßen gleich viele aneinander. Die Bezeichnungen sind analog zu vorhin: 82·4 bedeutet z.B., dass um eine Ecke zwei Achtecke und ein Viereck liegen.
Man kann aus einer regulären Kachelung eine halbreguläre erhalten, indem man allen Vielecken die Ecken abschneidet - so entsteht z.B. aus 63 das Muster 6·3·6·3 (1. Reihe links). Wenn man ein bisschen weniger abschneidet, wird aus einem n-Eck ein 2n-Eck - so erhält man z.B. aus 44 das bekannte Fussbodenmuster 82·4 (2. Reihe links). Eine weiter Möglichkeit ist es, die ursprünglichen Kacheln etwas auseinander zu ziehen und dazwischen Quadrate einzufügen (1. Reihe rechts). Und schließlich kann man die auseinandergezogenen Kacheln noch ein bisschen verdrehen und die Zwischenräume mit gleichseitigen Dreiecken ausfüllen (2. Reihe rechts).
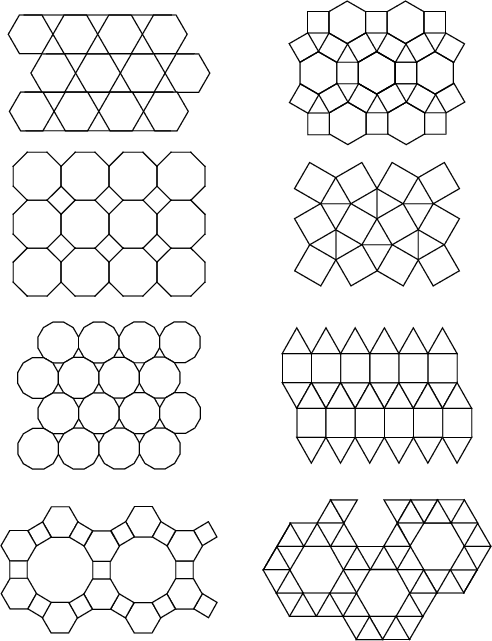
Auch zu jeder halbregulären Kachelung gibt es ein duales Muster. Es besteht aus lauter gleichen Kacheln - diese sind allerdings keine regelmäßigen Polygone. Die dualen Muster zu allen regulären und halbregulären Kachelungen findet ihr auf http://mathworld.wolfram.com/DualTessellation.html. (Von dieser Seite stammen auch die obigen Abbildungen.)
Wenn man nicht verlangt, dass alle Ecken gleich aussehen, findet man noch einige teilreguläre Kachelungen. Eine Auswahl davon könnt ihr auf http://mathworld.wolfram.com/DemiregularTessellation.html bewundern.
Alle diese Muster sind periodisch, das heißt, sie wiederholen sich in regelmäßigen Abständen. Roger Penrose (geb. 1931) entdeckte, dass es auch aperiodische Parkettierungen gibt, also Muster, die die ganze Ebene ausfüllen, ohne sich je zu wiederholen. So kann man z.B. mit regelmäßigen Fünfecken die Ebene nicht ausfüllen, aber aus zwei Rauten mit den Winkeln 36° bzw. 72° (Winkeln, die auch beim regelmäßigen Fünf- bzw. Zehneck auftreten) kann man die ganze Ebene bedecken. So ein Penrose-Parkett hat einen eigenen ästhetischen Reiz - ein Beispiel seht ihr auf http://tech-www.informatik.uni-hamburg.de/Personal/hendrich/penrose/penrose.html.
Hier findet ihr noch mehr zum Thema: http://www.mathematische-basteleien.de/parkett.htm. (Die Bezeichnungen sind etwas anders.) Und hier ist eine englische Seite über Kachelungen: http://mathforum.org/sum95/suzanne/whattess.html. Dort findet ihr auch weiterführende Links.
Übrigens (das gehört jetzt nicht ganz zum Thema "Regelmäßige Vielecke") haben Parkettierungen auch den holländischen Künstler M. C. Escher (1898 - 1972) fasziniert. Viele seiner Werke findet ihr auf der offiziellen Escher-Website: http://www.mcescher.com/ (sucht am besten in der Galerie unter "Symmetry".)
Nächstes Mal wird es darum gehen, welche Körper man aus regelmäßigen Vielecken aufbauen kann. Bis dahin wünsche ich euch frohe Weihnachten, einen guten Rutsch ins neue Jahr und viel Freude mit der Geometrie!
Jutta
E-mail: gut.jutta.gerhard@chello.at