
Nr. 5 / Jänner 2005
Im letzten Newsletter haben wir uns mit regelmäßigen Vielecken beschäftigt. Heute wollen wir einige Körper ansehen, die man daraus aufbauen kann. Einen Körper, der von ebenen Flächen begrenzt wird, bezeichnet man als Polyeder (Vielflächner). Wir interessieren uns hier für symmetrische Polyeder.
(Die Abbildungen findet ihr vor allem in den Links - schaut bitte alle an!)
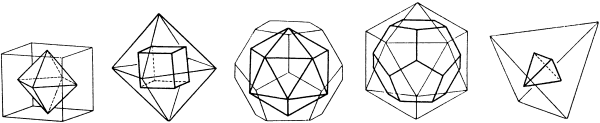
Am meisten symmetrisch sind Körper, die aus lauter gleichen regelmäßigen Vielecken bestehen, wobei in jeder Ecke gleichviele Flächen aneinanderstoßen. Diese Körper heißen Platonische Körper (nach dem griechischen Philosophen Plato, der sich auch viel mit Geometrie beschäftigt hat). Euklid hat sie im XIII. Buch seiner "Elemente" beschrieben. Wir können sie als dreidimensionales Gegenstück zu den regulären Kachelungen betrachten.
Man kann sich leicht überlegen, dass es nur fünf solche Körper geben kann: um eine Ecke zu bilden, braucht man mindestens drei Flächen, wobei die Winkelsumme weniger als 360° betragen muss. Daher kommen nur folgende Möglichkeiten in Frage: drei, vier oder fünf gleichseitige Dreiecke, drei Quadrate oder drei regelmäßige Fünfecke. Alle anderen Kombinationen haben eine Winkelsumme von 360° oder mehr.

Wir bezeichnen die regelmäßigen Polyeder so wie die Kachelungen: nm soll bedeuten, dass in jeder Ecke m regelmäßige n-Ecke aneinandergrenzen. Es gibt folgende Körper (E ist die Anzahl der Ecken, K die der Kanten und F die der Flächen):
| Name | |
| | |
| Tetraeder | | |
| |
| Würfel (Hexaeder, Kubus) | |
| |
|
| Oktaeder | | |
| |
| Ikosaeder | | |
|
|
| Dodekaeder | | |
| |
Diese Namen werden aus den griechischen Zahlworten gebildet und beziehen sich immer auf die Anzahl der Seitenflächen, ein Oktaeder (griech. okto: acht) hat z.B. 8 Seitenflächen.
Die platonischen Körper erfüllen, ebenso wie alle andern Polyeder, die Eulersche Polyederformel:
E + F - K = 2
Wenn man die Mittelpunkte der Seitenflächen eines Würfels miteinander verbindet, erhält man ein Oktaeder und umgekehrt. Diese beiden Körper hängen also zusammen, sie sind dual zueinander. Ebenso sind Ikosaeder und Dodekaeder duale Körper. Das Tetraeder ist zu sich selbst dual.
Auf http://www.uwgb.edu/dutchs/symmetry/platonic.htm wird der Zusammenhang zwischen platonischen Körpern und Kachelungen dargestellt.
Johannes Kepler glaubte, dass die platonischen Körper den Aufbau des Sonnensystems bestimmten. Er nahm an, dass sich die Planeten auf Kugelschalen bewegten, zwischen denen man platonische Körper einschreiben könne. (Eine Abbildung dazu findet ihr auf http://btmdx1.mat.uni-bayreuth.de/~rockstroh/geschichte_frameset.htm unter "Kepler".) Später kam er allerdings von dieser Theorie ab, weil er entdeckte, dass die Planetenbahnen Ellipsen sind.
(Ein paar Bemerkungen noch zur Bezeichnung "Würfel": dieses Wort kommt von "werfen"; es bezieht sich also nicht auf die Form, sondern darauf, dass man ihn bei vielen Spielen wirft. Im normalen Sprachgebrauch bezeichnet es einen Kubus. Bei Rollenspielen gibt es aber auch 8-, 12-, 20- und mehrseitige "Würfel". Eine Auswahl findet ihr auf http://www.Wuerfel-Offensive.de, z.B. unter "Standardwürfel".)
Als nächstes betrachten wir die Körper, die man aus verschiedenen regelmäßigen Vielecken zusammensetzen kann. Dabei sollen aber alle Ecken gleich aussehen. Diese Körper wurden von Archimedes untersucht. Es gibt 13 von ihnen - ihr findet sie auf http://www.uwgb.edu/dutchs/symmetry/archpol.htm.
Man erhält die archimedischen Körper aus den platonischen, indem man die Ecken abschneidet (z.B. 1. Reihe links: abgestumpfter Würfel) oder die Seitenflächen auseinanderzieht und dazwischen Quadrate einfügt (z.B. 1. Reihe rechts: kleines Kubo-Rhombi-Oktaeder). Wenn man die auseinandergezogenen Seitenflächen etwas verdreht und die Zwischenräume mit Dreiecken ausfüllt, erhält man zwei merkwürdig "schiefe" Körper (3. Reihe: schiefer Würfel, schiefes Dodekaeder). Wir können die archimedischen Körper als dreidimensionales Gegenstück zu den halbregulären Kachelungen betrachten.
Auch zu den archimedischen Körpern gibt es duale Körper. Diese werden allerdings nicht mehr von regelmäßigen Vielecken, sondern von gleichschenkeligen Dreiecken, Rhomben oder Drachenvierecken begrenzt. Hier sind sie abgebildet: http://mathworld.wolfram.com/ArchimedeanDual.html.
Genaueres zu den archimedischen Körpern findet ihr auf http://www.wissenschaft-online.de/artikel/709798, Folge 10.Wenn man auch Gebilde wie den Drudenfuß (einen fünfzackigen Stern) als Seitenflächen zulässt und erlaubt, dass die einzelnen Flächen einander durchdringen, kann man weitere vier regelmäßige Körper finden. Zwei von ihnen hat Johannes Kepler untersucht, die anderen beiden wurden erst zu Beginn des 19. Jahrhunderts vom französischen Mathematiker Louis Poinsot entdeckt. So sehen sie aus: http://www.uwgb.edu/dutchs/symmetry/kpsolid.htm.
Das kleine Sterndodekaeder kannte schon der italienische Renaissancemaler Paolo Uccello. Er hat es auf einem Fußbodenmosaik in der Eingangshalle des Markusdoms in Venedig dargestellt: http://www.math-inf.uni-greifswald.de/mathematik+kunst/uccello.html.
Zu diesem faszinierenden Thema könnte man noch viel mehr schreiben. Ich will euch daher noch auf einige interessante Websites hinweisen:
Auf der Seite von "Spektrum der Wissenschaft" gibt es eine Serie zur räumlichen Geometrie: http://www.wissenschaft-online.de/artikel/709798. Unbedingt anschauen!
Auf der Homepage der Universität Bayreuth gibt es eine Seite über platonische Körper: http://btmdx1.mat.uni-bayreuth.de/~rockstroh/Platon.htm. Hier erfahrt ihr auch einiges über die platonischen Körper in der Geschichte, Kunst und Natur.
Auf der amerikanischen Seite "Symmetry, Crystals and Polyhedra" (http://www.uwgb.edu/dutchs/symmetry/symmetry.htm) geht es um Kristalle, Kachelungen (das Thema des letzten Newsletters) und um viele Arten von Polyedern, von denen ich hier nur die wichtigsten vorgestellt habe.
Viel zu sehen gibt es auch auf der Seite von Fr. Magnus Wenninger: http://www.employees.csbsju.edu/mwenninger/. Das ist ein Benediktinerpater, der viele originelle Polyedermodelle gebaut hat.
Und wenn ihr jetzt Lust bekommen habt, selbst Modelle zu basteln, findet ihr auf http://www.korthalsaltes.com/index_hoofd.html die Schnittmuster dazu.
Viel Spaß!
Jutta
E-mail: gut.jutta.gerhard@chello.at