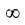für "unendlich" wurde von
John Wallis (1616-1703) eingeführt. Es ist wahrscheinlich eine Abwandlung des
römischen Zahlzeichens M.)Nr. 6 / Februar 2005
Wie der Leiter des GIMPS-Projekts (Great Internet Mersenne Prime Search) am 18. Februar bekanntgegeben hat, ist schon wieder eine neue Primzahl entdeckt worden. Es handelt sich um die 42. Mersennesche Primzahl (siehe Newsletter 3). Die Zahl selbst wurde noch nicht veröffentlicht (sie muss erst überprüft werden); man weiß aber, dass sie zwischen 7 und 10 Millionen Stellen hat. (Nähere Informationen: http://mathworld.wolfram.com/news/2005-02-18/mersenne/)
Dieses Zahlenmonster ist die größte derzeit bekannte Primzahl. Aber wie schon Euklid vor 2300 Jahren bewiesen hat, gibt es unendliche viele Primzahlen. Euklid vermeidet allerdings den Ausdruck "unendlich"; er schreibt: "Es gibt mehr Primzahlen als jede vorgelegte Anzahl von Primzahlen" (Elemente IX, § 20). Das bringt uns auf unser heutiges Thema:
Die Mathematik wird gern als "Wissenschaft vom Unendlichen" bezeichnet. Andrerseits gibt es keine einzige unendlich große Zahl - alle Zahlen, mit denen in der Mathematik gerechnet wird, haben einen bestimmten, endlichen Betrag. Was hat es also mit dem Begriff "unendlich" auf sich? Um das herauszufinden, müssen wir zuerst eine andere Frage klären:
Überlegen wir uns einmal, wie ein kleines Kind die Zahlen lernt. Es sieht beispielsweise verschiedene Gruppen von Objekten: 3 Personen (Mama, Papa, ich), 3 Sessel, 3 Teller, 3 Löffel, ... Mit der Zeit kommt es drauf, dass alle diese Gruppen (ein Mathematiker würde sagen: Mengen) eine gemeinsame Eigenschaft haben: ihre Anzahl. Egal, in welcher Reihenfolge die Objekte gezählt werden, das Zählen endet immer bei 3. Diese abstrakte Eigenschaft ist die Zahl 3.
Die natürlichen Zahlen sind also bereits abstrakte Begriffe. Die Zahl 3 kommt in der Natur nirgends vor!
Die Mathematiker können nun die Eigenschaften dieser Zahlen untersuchen. Sie können sie addieren, multiplizieren, potenzieren und mit ihnen Gleichungen lösen. Jedesmal, wenn dabei Probleme auftauchen, die im bisherigen Zahlbereich nicht gelöst werden können, führen sie neue Zahlen, also neue abstrakte Objekte, ein. So führt z.B. die Gleichung
x + 5 = 2 zu den negativen Zahlen,
4x = 3 zu den Brüchen,
x² = 2 zu den irrationalen Zahlen und
x² = -1 zu den komplexen Zahlen.
Trotz des bekannten Ausspruchs von Leopold Kronecker (1823 - 1891): "Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk" sind alle diese Zahlen nicht "unnatürlicher" als die "natürlichen Zahlen": sie sind abstrakte Gebilde, die nach bestimmten Regeln definiert werden. Allerdings eignen sie sich ausgezeichnet dazu, bestimmte Aspekte der Wirklichkeit zu beschreiben!
Eine Eigenschaft der natürlichen Zahlen ist nun, dass es unter ihnen keine größte gibt. Man kann ja zu einer gegebenen Zahl immer 1 addieren und so eine noch größere erhalten. Eine Menge mit 10100 Elementen kann sich niemand vorstellen, wir wissen nicht, ob es so etwas in der Realität überhaupt gibt (die Anzahl der Atome im Universum wird auf ca. 1080 geschätzt). Aber es ist logisch völlig einleuchtend, dass es eine größere Zahl als 10100 gibt, nämlich 10100+1. Wir können daher mit Euklid sagen: "Es gibt mehr natürliche Zahlen als jede vorgelegte Anzahl von natürlichen Zahlen", oder kürzer: Es gibt unendlich viele natürliche Zahlen.
(Übrigens: Das Zeichen 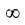für "unendlich" wurde von
John Wallis (1616-1703) eingeführt. Es ist wahrscheinlich eine Abwandlung des
römischen Zahlzeichens M.)
Gibt es eigentlich mehr natürliche als gerade Zahlen? Im ersten Moment würde man mit "Ja" antworten, weil ja nur jede zweite natürliche Zahl gerade ist. Andrerseits gibt es unendlich viele gerade Zahlen. Wie soll man verschiedene unendliche Mengen miteinander vergleichen?
Stellen wir uns noch einmal das kleine Kind vor. Auch wenn es noch nicht bis 3 zählen kann, kann es herausfinden, ob gleich viele Teller und Löffel da sind: es legt einfach zu jedem Teller einen Löffel und schaut, ob etwas übrigbleibt. Diese Methode können wir verallgemeinern. Georg Cantor (1845 - 1918), der Begründer der Mengenlehre, hat dafür den Begriff "Mächtigkeit einer Menge" eingeführt: Zwei Mengen haben die gleiche Mächtigkeit, wenn man jedem Element der einen Menge genau ein Element der anderen Menge zuordnen kann und umgekehrt. (Eine solche Zuordnung nennt man bijektiv.) Nach dieser Definition sind die Mengen N (natürliche Zahlen) und Ng (gerade natürliche Zahlen) gleichmächtig, denn wir können jeder natürlichen Zahl ihr Doppeltes zuordnen:
1 2 3 4 5 ... 2 4 6 8 10 ...
Dasselbe gilt auch für die Primzahlen, die Quadratzahlen, die Kubikzahlen usw. Man bezeichnet solche Mengen auch als abzählbar unendlich, denn man kann ihre Elemente in einer Liste anordnen und "abzählen". (Natürlich kommt man damit nie an ein Ende, aber es ist sichergestellt, dass jedes Element beim Abzählen drankommt, d.h. eine bestimmte Nummer bekommt.) Auch die Menge der ganzen Zahlen können wir in einer solchen Liste anordnen:
0, 1, -1, 2, -2, 3, -3, ...
Alle diese Mengen haben also die gleiche Mächtigkeit wie die natürlichen Zahlen.
Cantor bezeichnet diese Mächtigkeit mit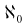 
("Aleph null"; Aleph ist der erste Buchstabe des hebräischen Alphabeths).
Aber was ist mit den rationalen Zahlen? Zwischen zwei ganzen Zahlen liegen doch unendlich viele Brüche, also müsste es viel mehr rationale als ganze Zahlen geben - oder? Cantor hat gezeigt, dass auch die rationalen Zahlen abgezählt werden können. Dazu schreiben wir sie so an:
1 2 3 4 5 ... 1/2 (2/2) 3/2 (4/2) 5/2 ... 1/3 2/3 (3/3) 4/3 5/3 ... 1/4 (2/4) 3/4 (4/4) 5/4 ... 1/5 2/5 3/5 4/5 (5/5) ... ... ... ... ... ... ...
Dann streichen wir alle Brüche, die schon gekürzt sind (in der Tabelle eingeklammert) und ordnen die übrigen entlang der Diagonalen:
1, 1/2, 2, 1/3, 3, 1/4, 2/3, 3/2, 4, 1/5, 5, ...
Wenn wir jetzt noch hinter jede Zahl die entsprechende negative schreiben und 0 an den Anfang der Liste setzen, haben wir eine Liste aller rationalen Zahlen. Auch die Menge der rationalen Zahlen hat also die selbe Mächtigkeit wie die natürlichen Zahlen.
Diese scheinbar paradoxen Ergebnisse werden am schönsten durch die Geschichte von "Hilberts Hotel" illustriert (nach David Hilbert (1862 - 1943), einem der bedeutendsten Mathematiker der Jahrhundertwende). Das ist ein Hotel mit abzählbar unendlich vielen Zimmern, die alle besetzt sind. Da kommt noch ein Gast an. Der Portier schafft es, ihn unterzubringen: er ersucht alle Gäste, in das Zimmer mit der nächsthöheren Nummer umzuziehen, und gibt dem neuen Gast Zimmer 1.
Nach einer Weile komnmt ein Autobus mit abzählbar unendlich vielen Gästen. Der Portier bringt auch diese unter, indem er jeden Gast in das Zimmer mit der doppelt so hohen Nummer verlegt - damit sind mit einem Schlag alle Zimmer mit ungeraden Nummern frei.
Sogar abzählbar unendlich viele Busse mit abzählbar unendlich vielen Insassen können untergebracht werden: man ordnet sie einfach entsprechend dem Diagonalverfahren an.
Nach diesen Ergebnissen könnte man fast glauben, dass alle Mengen abzählbar sind. Aber Cantor konnte auch beweisen, dass die Menge der reellen Zahlen (also aller Punkte der Zahlengeraden) nicht abzählbar ist. Eine reelle Zahl definierte er einfach als unendliche Dezimalzahl. (Diese Definition ist nicht ganz unproblematisch - damit werden wir uns in der nächsten Nummer beschäftigen.) Nun führte er einen Widerspruchsbeweis:
Angenommen, es gäbe eine Liste, die ALLE reellen Zahlen zwischen 0 und 1 enthält. Diese Zahlen hätten die Dezimaldarstellung
a = 0, a1 a2 a3 a4 a5 ...
b = 0, b1 b2 b3 b4 b5 ...
c = 0, c1 c2 c3 c4 c5 ...
d = 0, d1 d2 d3 d4 d5 ...
e = 0, e1 e2 e3 e4 e5 ...
...
(Die Buchstaben stehen für die einzelnen Dezimalstellen.)
Dann könnten wir eine neue Zahl bilden, nennen wir sie x, indem wir die erste Nachkommastelle der ersten Zahl, die zweite Stelle der zweite Zahl usw. nehmen:
x = 0, a1 b2 c3 d4 e5 ...
Nun ändern wir JEDE Stelle dieser "Diagonalzahl" ab, z.B. indem wir vereinbaren: Wenn an der entsprechenden Stelle von x eine 0 steht, ersetzen wir sie durch 1, alle anderen Ziffern werden durch 0 ersetzt. Die so entstandene Zahl nennen wir z.
z ist also eine reelle Zahl zwischen 0 und 1, aber sie kann nicht in der Liste stehen. Denn sie unterscheidet sich von a an der ersten Stelle, von b an der zweiten, ... von der n-ten Zahl der Liste an der n-ten Stelle usw. Die Liste kann also - im Widerspruch zur ursprünglichen Annahme - nicht alle reellen Zahlen zwischen 0 und 1 enthalten.
Wenn schon die reellen Zahlen zwischen 0 und 1 nicht abzählbar sind, dann erst recht
nicht alle reellen Zahlen. Die Menge R hat also eine größere Mächtigkeit als die Menge N.
Man könnte sagen: Es gibt "mehr" reelle als natürliche Zahlen.
Es ist eine ungeklärte Frage, ob die Mächtigkeit des Kontinuums (also der reellen Zahlen)
gleich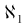 
, der nächsthöheren Stufe nach
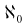ist, oder ob es noch Mengen gibt, die dazwischen
liegen. Hilbert zählte dieses Problem (die "Kontinuumshypothese") zu den wichtigsten
Problemen, denen sich die Mathematik im 20. Jahrhundert widmen sollte. Seit 1963 weiß man,
dass die Frage im Rahmen der Mengenlehre unentscheidbar ist (d.h., man kann diese Hypothese
weder beweisen noch widerlegen).
Haben wir mit 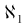die höchste Stufe der Unendlichkeit
erreicht? Nein, denn man kann zeigen, dass die Potenzmenge einer Menge (also die Menge ihrer
Teilmengen) immer eine höhere Mächtigkeit hat als die Menge selbst. Im Endlichen ist das einleuchtend:
eine Menge mit 3 Elementen, etwa M = {a, b, c}, hat folgende Teilmengen:
{ }, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c},
also insgesamt 23 = 8 Teilmengen. Dass diese Aussage auch im Unendlichen gilt, kann ebenfalls mit einem Widerspruchsbeweis gezeigt werden. Dieser Beweis läuft im Wesentlichen auf das Paradox vom Dorfbarbier hinaus, der alle Männer im Dorf rasiert, die sich nicht selbst rasieren. Rasiert der Barbier sich selbst? (Wer den Beweis nachlesen will, findet ihn hier.)
Wir haben also gesehen: Zahlen sind immer endlich, aber die Mächtigkeit einer Menge kann unendlich sein - es gibt sogar unendlich viele Stufen von unendlichen Mächtigkeiten!
In einigen Gebieten der Mathematik, vor allem in der Differential- und Integralrechnung, spielen "unendlich kleine" Größen eine Rolle. Darauf möchte ich im nächsten Newsletter eingehen.
Bis dahin alles Gute
Jutta
E-mail: gut.jutta.gerhard@chello.at