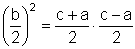
Nr. 9 / Juli 2005
Diesmal hat es etwas länger gedauert. Ich hatte mit Prüfungsvorbereitungen und -korrekturen ziemlich viel zu tun. Aber jetzt habe ich Ferien und mehr Zeit :-) Und noch eine gute Nachricht: Der Newsletter hat schon über 100 Abonnenten!
Das heutige Thema kommt aus der Geometrie, aber es hat eigentlich mehr mit Zahlentheorie zu tun. Es geht um bestimmte Dreiecke, deren Seitenlängen ganze Zahlen sind.
Eine der ältesten und bekanntesten mathematischen Formeln ist der Satz von Pythagoras: In einem rechtwinkeligen Dreieck ist das Quadrat der Hypotenuse gleich der Summe der Quadrate der Katheten, in Kurzform:
a² + b² = c²
Dieser Satz war schon den babylonischen, indischen und chinesischen Mathematikern bekannt. Sie wußten auch, dass ein Dreieck mit den Seitenlängen 3, 4 und 5 rechtwinkelig ist, denn 3² + 4² = 5². In indischen Texten kommen auch einige andere rechtwinkelige Dreiecke mit ganzzahligen Seitenlängen vor, und auf einem babylonischen Tontäfelchen (Plimpton 322) findet sich sogar eine Liste von 15 solcher Dreiecke.
Wir wollen jetzt untersuchen, wie man solche Dreiecke finden kann. (Im Allgemeinen erhät man ja, wenn man zwei Seiten beliebig wählt, für die dritte irgendeine Wurzel.) Ein Tripel (a, b, c) von drei ganzen Zahlen, die die Gleichung a² + b² = c² erfüllen, heißt pythagoräisches Tripel, und ein Dreieck mit diesen Seitenlängen bezeichnen wir als pythagoräisches Dreieck. Wenn man alle drei Zahlen mit demselben Faktor multipliziert, erhält man natürlich wieder ein pythagoräisches Tripel. Wir wollen zunächst nur solche Tripel betrachten, bei denen a, b und c keinen gemeinsamen Teiler haben (wenn es einen gibt, können wir durch ihn dividieren). Das heißt, dass a und b nicht beide gerade sein können, sonst wäre auch c gerade, und wir könnten durch 2 kürzen. Sie können aber auch nicht beide ungerade sein. Denn das Quadrat einer geraden Zahl ist durch 4 ohne Rest teilbar, das Quadrat einer ungeraden Zahl mit Rest 1. Wären a und b ungerade, so hätte c² bei der Division durch 4 den Rest 2, und das ist unmöglich. Wir nehmen daher an, dass a ungerade und b gerade ist; c muss dann ungerade sein.
Wir formen nun die Gleichung ein bisschen um:
b² = c² - a² = (c + a)(c - a)
c + a und c - a müssen gerade sein, daher können wir die ganze Gleichung durch 4 dividieren:
Weil a und c keinen gemeinsamen Teiler haben, haben auch c + a und c - a keinen gemeinsamen Teiler. Ihr Produkt kann nur dann eine Quadratzahl sein, wenn die beiden Faktoren selbst Quadratzahlen sind (das wird in der Zahlentheorie gezeigt). Wir setzen also
Daraus können wir jetzt a, b und c berechnen:
a = u² - v²
b = 2uv
c = u² + v²
Wenn wir jetzt für u und v beliebige ganze Zahlen einsetzen, erhalten wir unendlich viele pythagoräische Tripel. Einige Beispiele:
u v a b c 2 1 3 4 5 3 2 5 12 13 4 1 15 8 17 4 3 7 24 25 5 2 21 20 29 5 4 9 40 41
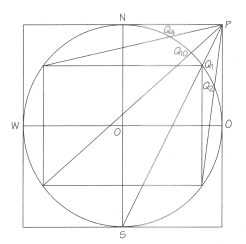Eine andere Methode, pythagoräische Tripel zu erhalten, beschreiben J. H. Conway und
R. Guy in ihrem Buch "Zahlenzauber". (Die nebenstehende Abbildung ist aus diesem Buch.)
Sie benutzen dazu einen Einheitskreis.
Man kann nämlich jedem Tripel (a, b, c) einen Punkt auf dem Einheitskreis mit den
Koordinaten (a/c / b/c) zuordnen und umgekehrt.
Verbindet man den Punkt P(1/1) mit S(-1/0), so schneidet die Verbindungsgerade den Kreis
in Q1(4/5 / 3/5) - das entspricht dem
Tripel (3, 4, 5). Wenn man diesen Punkt an den Kooordinatenachsen spiegelt und die neuen
Punkte wieder mit P verbindet, erhält man aus den neuen Schnittpunkten die Tripel (5, 12, 13),
(8, 15, 17) und (20, 21, 29). Wenn man den Vorgang wiederholt, erhält man alle pythagoräischen
Tripel.
Der griechische Geometer Heron von Akexandria (1. Jh. n. Chr.) bewies folgende Formel:
Damit kann man den Flächeninhalt eines beliebigen Dreiecks berechnen, wenn man die Seitenlängen kennt. Dabei ist s der halbe Umfang.
Ein Dreieck, bei dem alle drei Seiten und der Flächeninhalt ganzzahlig sind, bezeichnen wir als Heronsches Dreieck. Wie kann man solche Dreiecke finden? Natürlich ist jedes pythagoräische Dreieck heronisch. (Die Fläche eines rechtwinkeligen Dreiecks beträgt a·b/2, und weil b gerade ist, ergibt das eine ganze Zahl.) Auch wenn man zwei gleiche pythagoräische Dreiecke aneinanderfügt, erhält man ein (gleichschenkeliges) Heronsches Dreieck.
Interessanter wird es, wenn wir verschiedene Dreiecke aneinanderfügen. Wenn wir zum Beispiel das (3, 4, 5)-Dreieck auf das Dreifache vergrößern und das (5, 12, 13)-Dreieck anfügen, erhalten wir ein Dreieck mit den Seitenlängen 15, 13 und 9 + 5 = 14. Der Flächeninhalt beträgt 84. Dieses Dreieck führt auch Heron als Beispiel an.
Wir können aber auch die beiden Dreiecke aufeinanderlegen und die kleinere Fläche von der größeren abziehen. Das Restdreieck hat dann die Seitenlängen 15, 13 und 9 - 5 = 4 und den Flächeninhalt 24.
Wir wollen nun wieder eine allgemeine Formel ableiten, aus der wir alle Heronschen Dreiecke erhalten können. Wir gehen aus von den beiden rechtwinkeligen Dreiecken mit den Seitenlängen
a = s² - t², b = 2st, c = s² + t² bzw.
d = u² - v², e = 2uv, f = u² + v²,
vergrößern das erste um den Faktor uv, das zweite um den Faktor st und fügen die Seiten b und e aneinander. Das neue Dreieck hat dann die Seitenlängen
x = uv(s²+ t²)
y = st(u² + v²)
z = uv(s² - t²) + st(u² - v²) = (su - tv)(sv + tu)
Wenn wir die Dreiecke aufeinanderlegen, hat das Restdreieck die Grundlinie
z' = uv(s² - t²) - st(u² - v²) = (su + tv)(sv - tu)
Aus jedem Quadrupel (s, t, u, v) von ganzen Zahlen erhalten wir also zwei verschiedene Heronsche Dreiecke. Wenn die Seiten einen gemeinsamen Teiler haben, können wir durch diesen kürzen.
Einige Beispiele (gemeinsame Teiler wurden gekürzt):
s t u v x b c A 3 2 2 1 13 15 14 84 13 15 4 24 3 1 3 2 20 13 21 126 20 13 11 66 5 1 2 1 52 25 63 630 52 25 33 330
Im Oktober 1847 schrieb der Astronom Heinrich Christian Schumacher an seinen Freund Carl Friedrich Gauß einen Brief, in dem er ihm ein interessantes Problem vorlegte. Er hatte in einem alten Mathematikbuch folgende Aufgabe gefunden:
"Drey Schützen A, B, C, steht jeder an einem besondern Ort nach einem Vogel oder Papegay zu schiessen, doch einer soweit als der andre vom Papegay, aber B von C, 66 Fuß; B von A, 50 Fuß, A von C, 104 Fuß. Man fragt wenn der Papagay von der Erden 156 Fuß erhöht ist, wieviel Fuß weit diese Schützen müssen schiessen, daß sie solchen Papegay erreichen?
Begreiflich stehn sie in den Winkelspitzen eines Dreyecks, der Kreis um das Dreyeck hat zum Halbmesser 65, über des Kreises Mittelpunkt ist der Vogel lothrecht 156, aus beyder Quadrate Summe die Wurzel gezogen, giebt die Weite jedes Schützens vom Vogel = 169."
Der Vogel sitzt also über dem Umkreismittelpunkt des Dreiecks ABC, der Umkreisradius beträgt 65 Fuß. Schumacher fragte sich nun, wie man Dreiecke finden könnte, bei denen alle drei Seitenlängen und der Umkreisradius ganze Zahlen sind. Ein solches Dreieck wollen wir Schumacherdreieck nennen.
Den Umkreisradius eines Dreiecks kann man aus folgender Formel berechnen:
Setzen wir hier die Gleichungen für Heronsche Dreiecke ein, die wir vorhin gefunden haben, so erhalten wir:
Wir können also aus jedem Heronschen Dreieck ein Schumacherdreieck erhalten, indem wir die Seitenlängen mit 4 multiplizieren. Das ergibt folgende Formeln:
x = 4uv(s²+ t²)
y = 4st(u² + v²)
z = 4(su - tv)(sv + tu) bzw.
z' = 4(su + tv)(sv - tu)
Diese Formeln (mit etwas anderen Bezeichnungen) notierte Gauß auf dem Umschlag des Briefes von Schumacher. Auch hier einige Beispiele (gemeinsame Teiler sind wieder gekürzt):
s t u v x b c R 3 2 2 1 104 120 112 65 104 120 32 65 3 1 3 2 120 78 126 65 120 78 66 65 5 1 2 1 104 50 126 65 104 50 66 65
In der letzten Zeile steht das Beispiel, das Schumacher angeführt hat. (Es fällt auf, dass der Umkreisradius 65 sehr oft vorkommt!)
Ich möchte hier meinen Dank an Hermann Kremer aussprechen, der in der Newsgroup de.sci.mathematik einen Artikel über dieses Problem veröffentlicht hat. Wenn es euch interessiert, könnt ihr hier die ganze Diskussion nachlesen.
Versucht doch selbst, mit den Formeln ein bisschen herumzuspielen. Vielleicht findet ihr ja interessante Beispiele! Ich wünsche euch einen schönen Sommer!
Bis zum nächsten Mal
Jutta
E-mail: gut.jutta.gerhard@chello.at
