Aufgaben zur Relativitätstheorie
Lösungen:
|
c) 3,9 Lichtjahre d) 99,38% der Lichtgeschwindigkeit Ausführliche Lösung1 RETOUR zu Aufgabe1 |
|
2) a) 0,42ms b) 60 m c) 0,25 ms d) 1,5–10–30 kg Ausführliche Lösung2 RETOUR zu Aufgabe2 |
|
3)
a) 66,6 ms b)
1,33 ms c) 400
m d) keine Änderung e)
9,4–10–27 kg Ausführliche Lösung3 RETOUR zu Aufgabe3 |
|
4) relative Frequenzänderung: Df/f = 1,1–10–14 absolute Frequenzänderung: Df= 6,6 Hertz Ausführliche Lösung4 RETOUR zu Aufgabe4 |
|
|
Ausführliche
Lösung:
|
1) a) Die Entfernung zum Stern
beträgt 4,5 Lichtjahre, d.h. mit Lichtgeschwindigkeit ist man 4,5 Jahre
dorthin unterwegs, also braucht man mit halber Lichtgeschwindigkeit doppelt
so lang (indirektes Verhältnis): 9 Jahre b) Die Astronauten an Bord des
Raumschiffes erleben eine Verkürzung der Zeit um den Faktor Daher ist die Zeit auf 9*0,866 = 7,8 Jahre verkürzt. c) Die Verkürzung der Strecke erfolgt mit
dem gleichen Faktor wie b): statt 4,5 Lichtjahre werden es nur mehr 4,5*0,866 = 3,9 Lichtjahre d) Damit das Raumschiff nur ein Jahr
dafür benötigt, müsste gelten: t’ = 1 und die Gleichung t’ = t* 1 = 9 * 0,1111 = 0,0123456 = –0,9876 54= 0,9938 = v/c |*c v = 0,9938 c = 99,38% der
Lichtgeschwindigkeit |
|
2) a) v = 0,8 c = 0,8*300 000 km/s = 240 000 km/s = 2,4–108 m/s Der Weg ist das Produkt aus Geschwindigkeit mal Zeit: s
= v*t è
die Zeit daher: t = s/v = 100
/ (2,4–108) = 4,17–10–7 s = 0,42 ms b) Die Strecke wird mit dem Faktor c) Die Zeit wird um den gleichen Faktor
verkürzt wie die Strecke: t’ = t*0,6 = 0,42ms * 0,6 = 0,25 ms d) Die Masse wird um den Kehrwert des Faktors vergrößert:
m’ = m / 0,6 = 9–10–31/ 0,6 = 1,5–10–30 kg |
|
3) a) Zeit = Weg/Geschwindigkeit = 20 000 / (0,9998*3–108) = 66,6 ms b)
Der Wurzelfaktor ist Die Zeit
von 66,6 ms wird auf t’ =
t*Wurzelfaktor =
66,6*0,02 = 1,33 ms heruntergedehnt.
Das geht
sich mit der mittleren Lebensdauer von 2ms aus! c) Die
Strecke von 20 km wird auf s’ =
s* Wurzelfaktor =
20 000 m * 0,02 = 400
m gekürzt d) In
seinem Ruhesystem ruht das Teilchen, daher keine Massenänderung! e) Diese
Masse ergibt sich aus m’ =
m/Wurzelfaktor = 1,88–10–28/0,02 = 9,4–10–27 kg |
|
4) Der Energieansatz geht
folgendermaßen: E = Epot + ELicht (vorher) = E’pot + E’Licht (nachher) E =
0 + h*f = mgh + h*f’
und da es gilt:
E=mc² und E=h*f è m =
E/c² = h*f /c² Bringt man den Term h*f’ nach links,
kann man dann h herausheben: h*f – h*f’ =
mgh = h*f/c²*gh è f–f’ = f /c² *gh è (f–f’)/f = Df/f = g*h/c² Daher ist die relative
Frequenzänderung Df /f = 10*100 / (9–1016) = 1,1–10–14 . Das ergibt bei Licht der Wellenlänge
500 nm die Frequenz: c=l*f è f =
c/l = 3–108/(500–10–9) = 6–1014 und Df = f*1,1–10–14 = 6–1014*1,1–10–14 = 6,6 Hertz
absolute Frequenzänderung (und das kann man sogar messen!) |
|
5) Die Energie-Masse-beziehung
ist nach Einstein: E=mc² - wobei hier die bewegte Masse m als Masse
gemeint ist. Umgeformt auf m ergibt sich: m = E/c². Die
Differenz zur Ruhemasse m0 ergibt die Massenzunahme: Dm = m–m0 = E/c²
– m0 = E/c² – E0/c² = DE /c² Die zugeführte Energie ist die kinetische Energie DE = mv²/2. Das ergibt: Dm = mv²/2c². Bei einer Masse von m0 =
1000 kg und der Geschwindigkeit v = 180 km/h = 50 m/s ergibt das die
Massenzunahme Dm = 1000*50²/(2*9–1016) = 1,39–10-11 kg |
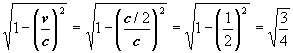 = 0,866.
= 0,866. 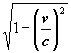 nach v aufgelöst werden:
nach v aufgelöst werden: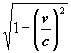
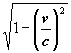
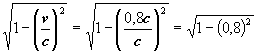 = 0,6 verkürzt. Daher wird daraus die Strecke: s’ =
s
= 0,6 verkürzt. Daher wird daraus die Strecke: s’ =
s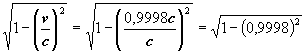 = 0,0199
= 0,0199