DES - Data Encryption Standard

Inhaltsverzeichnis:

  1. Symmetrische Kryptologie
    2.
  2. Geschichtliches
    3.
  3. Algorithmus
    4.
  4. Stärken & Schwächen
    5.
  5. Betriebsmodi
    6.
  6. Glossar
    7.

1. Symmetrische Kryptologie

Das Wesen symmetrischer Verschlüsselungsverfahren beruht darauf, dass ein und derselbe Schlüssel sowohl zur Ver- als auch zur Entschlüsselung dienen. Das Problem dieser Verfahren ist der Austausch und die Geheimhaltung der Schlüssel, die dem Sender und dem Empfänger bekannt sein müssen.

Inhaltsverzeichnis

2. Geschichtliches

1972 hat das NBS (National Bureau of Standards) ein Projekt ins Leben gerufen, um einen einzigen, für jeden zugänglichen Verschlüsselungsstandard zu entwickeln. Dieser Standard muss folgenden Punkten entsprechen:

Rückmeldungen verschiedenster Art zeigten, dass ein großer Teil der Bevölkerung sich für einen derartigen Standard interessierten, aber leider waren nur wenig Fachleute darunter, die in der Lage gewesen wären, einen solchen Standard zu entwickeln.
Ein zweiter Anlauf wurde am 27. August 1974 gestartet, wobei sich ein vielversprechender Kandidat ergab, ein Algorithmus, der auf der IBM-Entwicklung Lucifer basierte.

Um die Sicherheit des Algorithmus zu testen wurde die NSA (National Security Agency) um Hilfe gebeten. IBM hatte auf diesen Algorithmus bereits ein Patent angemeldet, war aber gewillt, ihr "intelektuelles Eigentum" anderen zur Verfügung zu stellen. Die NBS erarbeitete mit IBM eine Lizenz, in der IBM auf seine "Hoheitsrechte" verzichtet und diesen Algorithmus zur freien Implementierung zur Verfügung gestellt hat.

Viele Leute beschwerten sich über die Einmischung der NSA, weil allgemein angenommen wurde, dass die NSA eine Hintertür in den Algorithmus eingebaut hat, um sich selbst Zugang zu verschlüsselten Daten zu verschaffen. Ein Kritikpunkt war die Reduzierung der Schlüssellänge von ursprünglich 128 Bit auf 56 Bit, ein anderer war das neue Design der S-Boxes.
Nichtsdestotrotz wurde dieser Algorithmus am 23. November 1976 zum Data Encryption Standard erklärt. Die ofizielle Beschreibung des Standards FIPS PUB 46, "Data Encription Standard", wurde am 15. Jänner 1977 publiziert.

Es gab später noch kleinere Modfikationen und Zusätze, wie zB FIPS PUB 81, "DES Modes of Operation" (1980) oder FIPS PUB 74, "Guidelines for Implementing and Using the NBS Data Encryption Standard" (1981). Das NBS hat auch einen Standard FIPS PUB 112 "Specifying DES for password encryption" und FIPS PUB 113, "Specifying DES for computer data authentication" entworfen.

Diese Standards waren die ersten publizierten, die von der NSA getestet waren. Die NSA hatte geglaubt, dass DES nur in Hardware implementiert werden würde, doch das NBS hatte genügend Informationen publiziert, um DES-Verschlüsselungsmechanismen auch in Software zu implementieren.

Dieser Standard wurde später vom American National Standard Institute (ANSI) angenommen und 1981 als DEA im Standard ANSI X3.92 festgelegt. ANSI hatet auch einen Standard für "Modes of operation" (ANSI X3.106) herausgebracht, der dem des NBS sehr ähnelte. Ein zusätzlicher Standard aus dem Hause ANSI behandelt Netzwerkverschlüsselung, nämlich Standard ANSI X3.105
ANSI's Financial Institution Retail Security Working Group entwickelte einen Standard für die DES-Verschlüsselung von PINs (Personal Identification Number) (ANSI X9.8)

Validierung:

Ein Teil des Standards inkludiert, dass NIST (National Institute for Standards and Technologi) die Implementierungen des DES validiert, um sicherzustellen, dass die Implementierung auch dem Standard entspricht. Bis 1994 wurden nur Hard- bzw. Firmwareimplementierungen validiert, da Softwareimplementierungen nicht im Standard vorgesehen waren.

Ein weiterer Teil des Standards sieht eine Überprüfung des DES alle 5 Jahre vor. 1987 sah das NBS 3 Wege und schlug diese vor:

1. Den Standard für weitere 5 Jahre übernehmen,
2. den Standard zurücknehmen, oder
3. den Standard zu überarbeiten
DES wurde für weiter 5 Jahre übernommen, obwohl es immer wahrscheinlicher wurde, dass der Standard durch rapid steigende Rechnerleistung geknackt werden hätte können.

Im Jahr 1992 gab es immer noch keine Alternative, somit wurde DES für weitere 5 Jahre zum Standard erklärt.

Inhaltsverzeichnis

 

3. Algorithmus

DES ist ein Blockchiffrieralgorithmus, der 64bit-Blöcke mit einem 64bit-Key ver- bzw. entschlüsselt. Jedes 8. bit (least significant bit) im Schlüssel wird übergangen bzw. als Parity-bit benutzt, daraus ergibt sich eine effektive Schlüssellänge von 56 Bit. Es gibt eine handvoll Schlüssel, die als schwache Schlüssel gelten; diese können jedoch leicht verhindert werden. Die gesamte Sicherheit liegt im Schlüssel.
Prinzipiell besteht der Algorithmus nur aus Permutationen und Substitutionen; der gesamte Ablauf benötigt insgesamt 16 Runden, die wie folgt aufgebaut sind:

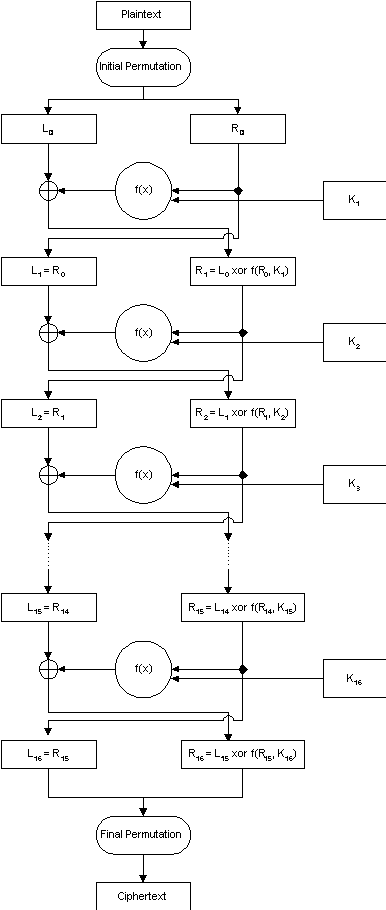
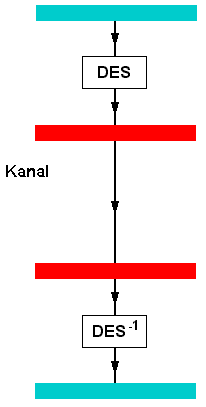
In obenstehender Grafik erkennt man den prinzipiellen Ablauf einer DES-Verschlüsselung. Nach der Initial Permutation werden die 64bit Blöcke in 32bit-Blöcke zerteilt; es ensteht eine linke und eine rechte Blockhälfte. Danach kommen 16 Runden mit identischen Operationen (hier Funktion f(x)), die die Daten mit dem Schlüssel kombimieren. Nach 16 Runden werden die linke und die Rechte Hälfte wieder vereint und nach der Final Permutation, die nichts anderes wie die inverse Funktion der Initial Permutation darstellt, erhält man den Chiffretext.
In jeder Runde wird aus dem 56bit Schlüssel ein 48bit Subschlüssel gewählt. Die rechte Datenhälfte wird auf 48 bits expandiert via einer Expansion Mutation, mit dem 48bit Subschlüssel kombiniert (XOR-function) und durch die sogenannten S-Boxes gesendet, deren Output 32 bits lang ist und die neue linke Datenhälfte darstellt.

3.1 Initial Permutation

58
50
42
34
26
18
10
2
60
52
44
36
28
20
12
4
62
54
46
38
30
22
14
6
64
56
48
40
32
24
16
8
57
49
41
33
25
17
9
1
59
51
43
35
27
19
11
3
61
53
45
37
29
21
13
5
63
55
47
39
31
23
15
7

Die Nummern dieser Tabelle entsprechen der Bitnummer (1..64) der zu verschlüsselnden Bitblöcke. Danach werden die ersten 32 bit der linken, die zweiten 32 bit der rechten Datenhälfte zugeordnet und die erste Verschlüsselungsrunde kann beginnen:

 

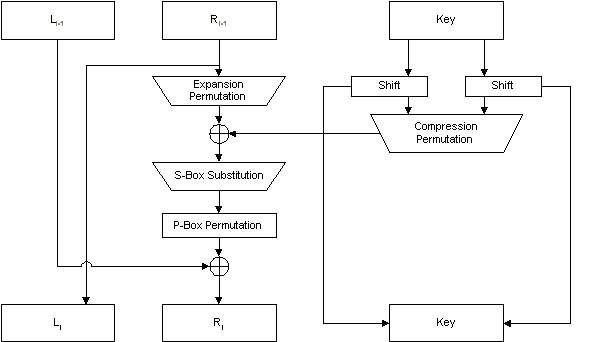
In dieser Grafik sieht man den Ablauf einer Runde DES mit allen dazugehörigen Operationen. Nach einem Key-Shift werden 48 bit aus dem 56bit Schlüssel gewählt. Dieses Verfahren wird Compression Permutation genannt, da aus ursprünglich 56 48 bit selektiert werden. Dieser Subschlüssel wird mit der expandierten rechten Datenhälfte xor-verknüpft und das so erhaltene Bitmuster durch die 8 S-Boxes geschickt. Nach einer P-Box Permutation wird das Ergebnis noch mit der linken Hälfte xor-verknüpft und die nächste DES-Runde kann beginnen.

Nach der 16. Runde wird noch eine Final Permutation durchgeführt, die nichts anderes darstellt, als die inverse Permutation zur Initial Permutation.

 

Number of Key Bits Shifted per Round:

Round
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Number
1
1
2
2
2
2
2
2
1
2
2
2
2
2
2
1

Diese Tabelle zeigt, in welcher Runde der Schlüssel wie oft geshiftet wird.

 

Key Permutation:

57
49
41
33
25
17
9
1
58
50
42
34
26
18
10
2
59
51
43
35
27
19
11
3
60
52
44
36
63
55
47
39
31
23
15
7
62
54
46
38
30
22
14
6
61
53
45
37
29
21
13
5
28
20
12
4

Diese Tabelle zeigt die Bitreihenfolge des 56 Bit langen Schlüssels, wobei jedes 8 Bit ignoriert wurde.

 

Compression Permutation:

14
17
11
24
1
5
3
28
15
6
21
10
23
19
12
4
26
8
16
7
27
20
13
2
41
52
31
37
47
55
30
40
51
45
33
48
44
49
39
56
34
53
46
42
50
36
29
32

Diese Tabelle zeigt die Permutation des 48 bittigem Subselects aus dem Schlüssel. Als Beispiel wird Bit #14 aus dem Schlüssel an erster, Bit #32 an letzer Stelle des Subselects stehen. Durch das Key-shifting in jeder Runde wird gewährleistet, dass jede Runde ein anderer Schlüssel verwendet wird.

3.2 Expansion Permutation

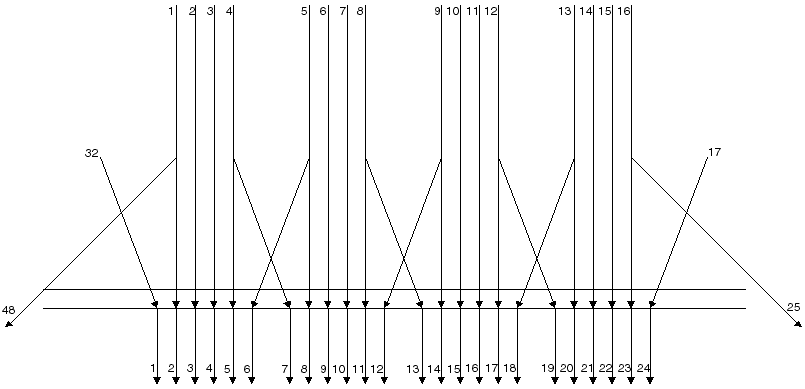
Diese Grafik verdeutlicht, wie die 16 Bit Input zu einem 24 Bit Output expandiert werden. Die Zahlen kennzeichnen die Bitnummern im In- bzw. Output.

3.3 S-Boxes (Substitution Boxes)

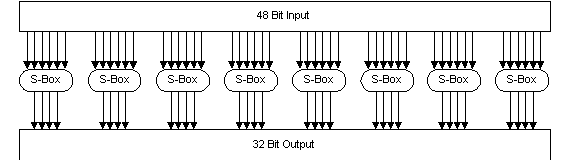
Diese Grafik erklärt schematisch die Funktionsweise der 8 S-Boxes, die jeweils 6 Bit Input und 4 Bit Output haben. Um den Output einer S-Box zu verstehen, muß man sich diese ein wenig genauer ansehen:

Eine S-Box ist eine Tabelle mit 16 Spalten und 4 Reihen, wobei jede S-Box andere Zahlenwerte hat. Die Zahlen haben alle 4 Bit. Der Input steht nun in einem ganz speziellen Zusammenhang mit einer Zahl in einer S-Box. Wenn ein 6bit Input b1,b2,b3,b4,b5 und b6 in eine S-Box geschickt wird, so stehen b1,b6 für die Reihe und b2,b3,b4,b5 für die Spalte in der Tabelle. So ergibt zB der Wert 110011 den Wert aus Reihe 11 (=3 bzw. 4.Reihe!) und Spalte 1001 (=9, Spalte 10!) und somit 1101 (=11). Man sollte nur nicht vergessen, bei 0 zu zählen anzufangen.

S-Box 1:
14
4
13
1
2
15
11
8
3
10
6
12
5
9
0
7
0
15
7
4
14
2
13
1
10
6
12
11
9
5
3
8
4
1
14
8
13
6
2
11
14
12
9
7
3
10
5
0
15
12
8
2
4
9
1
7
5
11
3
14
10
0
6
13

Diese Substitution ist der kritische Schrit in DES. Alle anderen Operationen des Algorithmus sind linear, diese ist nicht-linear und gibt DES seine Sicherheit.

3.4 P-Boxes (Permutation Boxes)

In den P-Boxes (Permutation Boxes) wird eine reine Permutation durchgeführt, kein Bit wird ignoriert, keines mehr als nur einmal verwendet. Jedem Inputbit ist exakt ein Outputbit zugeordnet:

16
7
20
21
29
12
28
17
1
15
23
26
5
18
31
10
2
8
24
14
32
27
3
9
19
13
30
6
22
11
4
25
Zum Beispiel Bit #21 schiebt sich an 4. Stelle, wobei Bit #4 auf Stelle 31 wandert.

 

3.5 Final Permutation:

Die Final Permutation stellt eine inverse Funktion zur Initial Permutation dar. Das Bitmapping wird in folgender Tabelle dargestellt:

40
8
48
16
56
24
64
32
69
7
47
15
55
23
63
31
38
6
46
14
54
22
62
30
37
5
45
13
53
21
61
29
36
4
44
12
52
20
60
28
35
3
43
11
51
19
59
27
34
2
42
10
50
18
58
26
33
1
41
9
49
17
57
25

Dies ist wieder eine reine Permutation, wobei kein Bit ignoriert bzw. mehrfach behandelt wird.

 

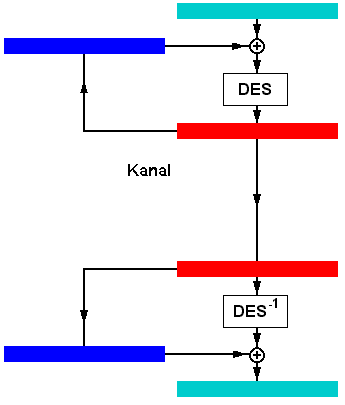
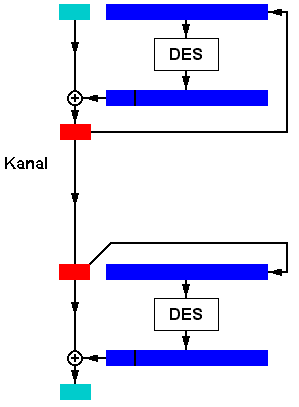
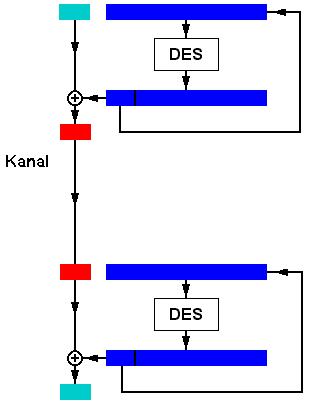
3.6 Entschlüsselung:

Nach all diesen Substitutionen, Permutationen XORs und Shifts bleibt die Frage, wie man einen verschlüsselten Text wieder lesen kann. Die Antwort ist einfach. DES arbeitet in beide Richtungen. Um einen Chiffre zu entschlüsseln, müssen nur oben genannte Schritte in umgekehrter Reihenfolge (auch die Runden, also 16,15,14,...3,2,1) durchgeführt werden.

Inhaltsverzeichnis

 

4. Betriebsmodi

4.1 ECB - Electronic Codebook Mode

ECB eignet sich nicht zur Übertragung langer Nachrichten.
Identische Klartextblöcke liefernt identische Chiffretextblöcke.
Chiffretextblöcke, die bei vorausgegangenen Übertragungen aufgezeichnet wurden, können eingefügt werden, um den Sinn einer Nachricht zu ändern.

4.2 CBC - Cipher Block Chaining Mode

JederChiffretextblock hängt vom vorhergehenden Chiffretextblock ab.
Identische Klartextblöcke liefern verschiedene Chiffretextblöcke.
Register werden bei Sender und Empfänger mit dem gleichen Wert initialisiert.

4.3 CFB - Cipher Feedback Mode

Der CFB ist die bevorzugte Methode um einzelne Zeichen zu verschlüsseln.
Sowohl sende- als auch empfangsseitig arbeitet der DES im Verschlüsselungsmodus.
Der DES wird zur kontinuierlichen Chiffre.
Klartexteinheiten haben eine Länge von 1 Bit bis 64 Bit.
der CFB ist nicht so effizient wie der CBC-mode.

4.4 OFB - Output Feedback Mode

Sowohl sende- als auch empfangsseitig arbeitet der DES im Verschlüsselungsmodus.
Übertragungsfehler wirken sich nur auf das betroffene Zeichen aus. Die Anwendung liegt bei der Übertragung auf Kanälen, auf denen Störungen zu erwarten sind, zB bei Satellitenverbindungen.
Problem der Synchronität, wenn Sender und Empfänger asynchron werden, kann der Rest der Nachricht nicht mehr entschlüsselt werden.

 

Inhaltsverzeichnis

 

5. Stärken & Schwächen

Die Sicherheit von DES wurde lange und oft in Frage gestellt; es gab etliche Diskussionen über Schlüssellängen, Rundenzahlen und über das Design von S-Boxes. Vor allem die S-Boxes bereiteten vielen Kopfzerbrechen - nur Konstanten, die "offensichtlich zufällig" angeordnet waren. IBM hingegen wehrte sich mit dem Argument, dass das Innenleben ein Ergebnis einer Arbeit von 17 Mannjahren war. Andere wiederum befürchteten, dass die NSA eine Hintertür in den Algorithmus eingebaut hat, um selber leichter an verschlüsselte Daten zu gelangen. Andere Stimmen wiederum ließen verlauten, dass die NSA sich ihrerseits gegen Hintertüren durch IBM abgesichert hat.

5.1 Schwache Schlüssel:

Weil der Schlüssel jede modifiziert wird um einen neuen Subschlüssel zu generieren, gibt es einige "schwache" Schlüssel, die die Sicherheit von DES nicht mehr gewährleisten. Da der Schlüssel zuerst geteilt wird, sind alle symmetrischen Schlüssel schwache Schlüssel. Zusätzlich gibt es ein paar Schlüssel, die aus dem selben Klartext den selben verschlüsselten Text generieren, dh man benötigt nicht den Originalschlüssel, um den Text zu entschlüsseln.
Doch bevor man dazu übergeht, DES wegen seiner "schwachen" Schlüssel zu kritisieren, sollte man bedenken, dass es insgesamt 64 "schwache" Schlüssel aus einem Schlüsselraum von 72 057 594 037 927 936 Schlüsseln gibt. Bei einem Zufallsschlüssel ist die Wahrscheinlichkeit, einen "schwachen" Schlüssel zu erhalten, vernachlässigbar.

5.2 Plaintext Attacks:

Die Chosen Plaintext Attack bei DES beruht darauf, dass ein komplementärer Schlüssel den komplementären Chiffretext bzw. der komplementäre Klartext denselben Chiffretext ergibt, was allerdings keine Besonderheit darstellt, da die Subkeys xor-verknüpft werden. Das einzige, was sich daraus ergibt, ist, dass ein Kryptoanalytiker nur die Hälfte der möglichen Schlüssel zu testen hat, also 2^55 statt 2^56. Eli Biham und Adi Shamir haben gezeigt, dass es eine Known Plaintext Attack derselben Komplexität gibt, die zumindesxt 2^33 Klartexte benötigt. Diese "Sicherheitslücke" ist eigentlich keine solche, weil es sehr unwahrscheinlich ist, dass in einem Klartext das entsprechende Komplement enthalten ist, bzw. kann man Benutzer davor warnen, komplementäre Schlüssel zu verwenden.

5.3 Algebraische Strukturen:

Jeder mögliche 64 Bit Block kann auf alle möglichen 64 Bit Chiffreblöcke in (2^64)! abgebildet werden. DES, mit seinem 56 Bit Schlüssel, enthält 2^56 (=~ 10^17) dieser Abbildungen und mit mehrfacher Verschlüsselung sogar mehr. Dies stimmt nur, wenn DES Operationen keine algebraische Strukturen erkennen lassen:

Falls DES abgeschlossen wäre, dann gäbe es für jeden Schlüssel K1 und K2 einen Schlüssel K3 für den gilt:

EK2(EK1(P)) = EK3(P)

Anders ausgedrückt, DES - Verschlüsselung würde eine abgeschlossene Gruppe bilden, und eine Verschlüsselung mit K1 gefolgt von einer Verschlüsselung mit K2 würde einen identisch verschlüsselten Text ergeben, als wäre dieser direkt mit K3 verschlüsselt worden.

Wenn DES rein wäre, würde es einen Schlüssel K4 geben, für den gilt:

EK3(EK2(EK1(P))) = EK4(P)

Somit wäre Dreifachverschlüsselung sinnlos. 1992 wurde bewiesen, dass DES keine Gruppe bildet und demnach keine algebraischen Strukturen enthält.

5.4 Differentielle Kryptoanalyse:

Eli Biham und Adi Shamir haben 1990 die differentielle Kryptoanalyse eingeführt, die sich speziell mit Paaren von verschlüsselten Texten, deren Klartexte wesentliche Unterschiede aufweisen, befasst. Diese Methode beobachtet die Entwicklung dieser Differenzen, die sich durch jede DES-Runde verändert, wenn beide Klartexte mit dem selben Schlüssel verschlüsselt worden sind.
Man muss nur zwei Klartexte mit einer fixen Differenz wählen (Differenz = XOR) und dann entsprechend der Differenz der Chiffretexts den Schlüsseln verschiedene Wahrscheinlichkeiten zuordnen. Bei genügend vielen Analysen wird ein Schlüssel sich als der wahrscheinlichste herausstellen, und dieser Schlüssel ist der richtige!

5.5 Lineare Kryptoanalyse:

Lineare Kryptoanalyse ist ein anderes Verfahren, dass von Mitsuru Matsui erfunden wurde. Diese Attacke verwendet lineare Approximation, um die Aktionen eines Blockchiffrieralgorithmus zu beschreiben. Das heißt nichts anderes, als dass einige Klartexte xor-verknüpft und einige verschlüsselte Texte xor-verknüpft und die Ergebnisse wiederum xor-verknüpft werden, und daraus erhält man ein Bit, das der xor-Verknüpfung einiger Schlüsselbits entspricht. Das ist eine lineare Annäherung und enthält eine gewisse Wahrscheinlichkeit p. Wenn p != 1/2 kann diese Eigenschaft ausgenutzt werden. Wie kann man nun DES damit knacken?

  1. Finde gute Rundenapproximationen und verknüpfe diese.
  2. Analysiere die S-Boxes (6 Bit Input, 4 Bit Output)

Die Inputbits können 63 verschiedene, sinnvolle Kombinationen haben (2^6-1), die Outputbits haben hingegen 15 verschiedene, sinnvolle Kombinationen. Für jede S-Box kann nun eine Wahrscheinlichkeit berechnet werden, sodass für einen zufälligen Input eine Input - xor - Kombination gleich einer Output - xor - Kombination ist. Falls es eine solche Eigenschaft gibt, wird die lineare Kryptoanalyse funktionieren.

 

6. Glossar

ANSI - American National Standard Institute, US-Amerikanische Standardisierungsorganisation

DEA - Data Encryption Algorithm, DES-Name von ANSI

DES - Data Encryption Standard

Lucifer - Blockchiffrierverfahren, in den 60ern von IBM entwickelt, mit Hilfe differentieller Kryptoanalyse kann Lucifer sehr schnell "geknackt" werden; Schlüssellänge: 128bit

NBS - National Bureau of Standards; siehe auch NIST

NIST - National Institute for Standards and Technology; US-Amerikanische Organisation, zuständig für technologische Standards

NSA - National Security Agency; US-Amerikanische Organisation, zuständig für sicherheitstechnische Fragen, bis in die 70er nahezu unbekannt wegen nationaler Geheimhaltung, hat daher auch den Beinamen "No Such Agency"