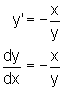
Trennung der Variablen:
y·dy = - x·dx
Integration:
ò y·dy = - ò x·dx
![]()
x2 + y2 = 2C
Ersetze 2C durch C1:
x2 + y2 = C1
Differentialgleichungen - Trennung der Variablen
Hier findest du einige einfache Differentialgleichungen, die du mit der Methode der "Trennung der Variablen" lösen kannst.
Beispiel:
|
|
|
|
Trennung der Variablen: |
y·dy = - x·dx |
|
Integration: |
ò y·dy = - ò x·dx
x2 + y2 = 2C |
|
Ersetze 2C durch C1: |
x2 + y2 = C1 |
Die Lösungen bilden eine Schar von konzentrischen Kreisen um den Koordinatenursprung.
Übungsbeispiele:
Löse die folgenden Differentialgleichungen durch Trennung der Variablen und skizziere die von den Lösungen gebildete Kurvenschar:
|
Differentialgleichung |
Lösung |
Kurvenschar |
|
|
1. |
y‘ = a× y |
y = k× eax |
Exponentialfunktionen |
|
2. |
y‘ = y2 |
|
Hyperbeln (in x-Richtung verschoben) |
|
3. |
y‘ = -xy |
y = k× e-x²/2 |
Gauss’sche Glockenkurven |
|
4. |
|
x2 - y2 = c |
Hyperbeln in Hauptlage |
|
5. |
|
y = kx |
Geraden durch den Ursprung |
|
6. |
|
|
Hyperbeln mit den Koordinatenachsen als Asymptoten |