Übungen: Exponentielle Wachstum- und Abnahmeprozesse

  1. Ein Kapital von 1000 € wird mit 8% Zinsen angelegt.
    1. In welcher Zeit verdoppelt sich das Kapital?
    2. Zeige, dass die Verdopplungszeit nicht davon abhängt, wie groß das Anfangskapital ist!

  2. Eine Bakterienkultur besteht zu Anfang aus 1000 Bakterien. Die Anzahl der Bakterien verdoppelt sich jede Stunde.
    1. Stelle die Anzahl der Bakterien nach t Stunden als Funktion der Zeit dar.
    2. Wieviele Bakterien sind nach 2,5 Stunden vorhanden?
    3. Wann wird sich die Anzahl der Bakterien verzehnfacht haben?
    4. Das Wachstum der Bakterien lässt sich durch die Formel
      N(t) = N0·eλt
      beschreiben (N0 = Anfangswert). Berechne die Konstante λ!

  3. Die Bevölkerung eines Landes wächst pro Jahr um 1,5%. Derzeit beträgt sie 12 Millionen.
    1. Wie groß wird die Bevökerung in 10 Jahren sein?
    2. Wann wird das Land 15 Millionen Einwohner haben?
    3. Der Bevölkerungszuwachs lässt sich durch die Formel
      N(t) = N0·eλt
      beschreiben. Berechne die Konstante λ!

  4. Angenommen, die Weltbevölkerung vermehrt sich nach der Formel
    N(t) = N0·eλt
    1960 gab es ca. 3 Mrd. Menschen, 1995 ca. 5,6 Mrd.
    1. Bestimme die Konstante λ!
    2. Wieviel Prozent beträgt das jährliche Wachstum der Weltbevölkerung?
    3. Wann wird die Erde 15 Mrd. Einwohner haben, wenn die Bevölkerung im selben Tempo weiterwächst?

  5. Vor 10 Jahren betrug der Holzbestand eines Waldes 7000 m³. Ohne Schlägerung ist er inzwischen auf 9880 m³ angewachsen. Man darf annehmen, dass das Holzwachstum ein exponentieller Vorgang ist.
    1. Zeige, dass die jährliche Wachstumsrate ca. 3,5% beträgt.
    2. Berechne die Zeitspanne, innerhalb der sich der Holzbestand verdoppelt bzw. verdreifacht.
    3. Man hat vor, in 3 Jahren 3000 m³ Holz zu schlägern. Wann wird dieser Wald den heutigen Holzbestand wieder erreichen?

  6. Ein Lichtstrahl, der ins Wasser fällt, wird pro Meter Wassertiefe um 10% schwächer.
    1. Stelle die Lichtstärke L(x) als Funktion der Wassertiefe dar (Tiefe in Metern = x, Lichtstärke an der Oberfläche = L0).
    2. Wie stark ist das Licht in 10 m Tiefe?
    3. In welcher Tiefe beträgt die Lichtstärke nur mehr ein Zehntel des ursprünglichen Wertes?

  7. Der radioaktive Zerfall eines Elements lässt sich durch die Formel
    N(t) = N0·e-λt
    beschreiben (N0 = Anfangswert). Die Zeit τ, in der von einer vorhandenen Stoffmenge die Hälfte zerfällt, heißt Halbwertszeit. Für Radium beträgt sie z.B. 1620 Jahre.
    1. Berechne die Zerfallskonstante λ!
    2. Wieviel war von dem ersten Gramm Radium, das Marie Curie 1898 herstellte, nach 100 Jahren noch übrig?
    3. Wann wird nur mehr 0,1 g vorhanden sein?

  8. Das Kohlenstoffisotop 14C zerfällt mit einer Halbwertszeit von ca. 5730 Jahren. Mit seiner Hilfe lässt sich das Alter von Fossilien bestimmen.
    1. Berechne die Zerfallskonstante λ!
    2. In einem Fossil wurde ein 14C-Gehalt von 7,5% der ursprünglichen Menge gemessen. Berechne das Alter des Fossils (runde auf 1000 Jahre).
    3. Bis zu welchem Alter lässt sich die 14C-Methode anwenden, wenn man noch 0,1% des ursprünglichen 14C-Gehalts mit hinreichender Genauigkeit messen kann?

  9. Vervollständige die folgende Tabelle:

    10. Element

    Halbwertszeit

    λ

    Abnahme pro Zeiteinheit in %

    Wann ist noch 1% übrig?

    Radium

    1620 Jahre

     

     

     

    Caesium 137

     

    0,0231 / Jahr

     

     

    Phosphor 32

     

    0,0485 / Tag

     

     

    Jod 131

    8 Tage

     

     

     

    Polonium 218

     

     

    20% / Minute

     

  10. Eine Tierpopulation hat sich in 5 Jahren von 200 auf 250 Tiere vergrößert. Wir nehmen zunächst an, dass die Vermehrung exponentiell erfolgt.
    1. Berechne die Konstante λ!
    2. Wieviel Prozent beträgt die jährliche Vermehrung?
    3. Wann hat sich die Population verdoppelt bzw. vervierfacht?

  11. (*) In der Realität ist unbegrenztes Wachstum nicht möglich. Wenn die Zahl der Tiere nach oben begrenzt ist (begrenztes Wachstum), lässt sich die Vermehrung besser durch folgende Gleichung beschreiben:
    N(t) = G - (G - N0)·e-λt
    (a ist der Anfangswert, G die obere Grenze)
    Angenommen, die Tierpopulation aus dem vorigen Beispiel vermehrt sich nach dieser Formel, G = 1000. Ermittle λ und berechne, wann sich die Population verdoppelt hat (ausgehend von 200 Tieren)!

  12. (*) Die beste Näherung erhält man durch folgende Gleichung (logistisches Wachstum):
    B(t) = N_0*G/(N_0 + (G-N_0)e^(-lambda*t))
    Mit den Angaben von Beispiel 10 und 11 erhält man: λ = 0,0575 (Kontrolle!)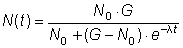
    Wie lange braucht die Population unter diesen Voraussetzungen, um sich zu verdoppeln?

  13. (*) Eine Tasse kochendheißer Kaffee (100° C) kühlt bei Zimmertemperatur (20° C) in 10 Minuten auf 30° C ab.
    1. Die Temperatur nach t Minuten wird durch die Gleichung
      T(t) = 20 + (T0 - 20)·e-λt
      angegeben. Berechne die Konstante λ!
    2. Frau M mischt den Kaffee mit der gleichen Menge Milch aus dem Kühlschrank (4° C). Sie hat zwei Möglichkeiten:
      • die Milch sofort dazugeben, danach 3 Minuten warten
      • die Milch erst nach 3 Minuten dazugeben
      Welche Temperatur hat der Milchkaffee in beiden Fällen?
      (Die Temperatur der Mischung ist der Mittelwert der einzelnen Temperaturen: T = (T1 + T2)/2.)

Ergebnisse

Zum Inhaltsverzeichnis