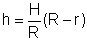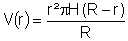Extremwertberechnungen
In der Praxis wird man oft vor die Aufgabe gestellt, eine Größe (Fläche, Volumen,
Materialverbrauch, Kosten... ) zu optimieren. Wenn wir die Größe durch eine Funktion
in einer Variablen ausdrücken können, können wir mit Hilfe der Ableitung den Extremwert
berechnen. Wenn mehrere Variablen vorkommen, müssen wir diese zuerst durch eine ausdrücken.
Schema zum Lösen einer Extremwertaufgabe:
- wenn möglich, Skizze zeichnen
- Zielfunktion: Größe, die maximal bzw. minimal werden soll
- wenn mehrere Unbekannte vorkommen: Nebenbedingung
(Formel, Pythagoras, Strahlensatz, Gleichung einer Kurve...)
- eine Unbekannte aus Nebenbedingung ausdrücken und in Zielfunktion einsetzen
- Vereinfachung der Zielfunktion:
- Konstante Faktoren dürfen weggelassen werden
- Die Zielfunktion darf quadriert werden
(nur positive Funktionswerte berücksichtigen)
- Man darf statt der Zielfunktion ihren Kehrwert betrachten
(Maximum wird zu Minimum und umgekehrt)
- (vereinfachte) Zielfunktion differenzieren
- 1. Ableitung = 0 setzen, Lösung berechnen
- Kontrolle durch 2. Ableitung
Beispiele:
-
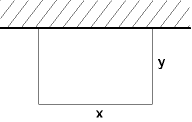
Entlang einer Mauer soll eine rechteckige Fläche von 50 m² eingezäunt werden. Wie lang
müssen die Seiten des Rechtecks sein, damit man möglichst wenig Zaun braucht?
| Zielfunktion: |
u(x,y) = x + 2y ® Minimum |
| Nebenbedingung: |
xy = 50
y = 50x-1 |
| einsetzen: |
u(x) = x + 100x-1 |
| differenzieren: |
u'(x) = 1 - 100x-2
u''(x) = 200x-3 |
| Minimum berechnen: |
1 - 100x-2 = 0
x = 10, y = 5 |
| Kontrolle: |
u''(10) = 200/1000 > 0 Þ Minimum |
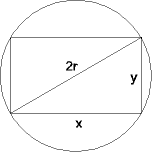
Welches von allen Rechtecken, die man einem Kreis vom Radius r einschreiben kann,
hat den größten Flächeninhalt?
| Zielfunktion: |
A(x,y) = xy ® Maximum |
| Nebenbedingung: |
x² + y² = 4r²
y = Ö(4r² - x²) |
| einsetzen: |
A(x) = x·Ö(4r² - x²) |
| vereinfachen: |
A~(x) = x²·(4r² - x²) = 4r²x² - x4 |
| differenzieren: |
A~'(x) = 8r²x - 4x³
A~''(x) = 8r² - 12x² |
| Maximum berechnen: |
8r²x - 4x³ = 0
x = rÖ2,
y = rÖ2 (Quadrat)
(x = 0 und die negative Lösung kommen nicht in Frage) |
| Kontrolle: |
A~''(rÖ2) = -16r² < 0
Þ Maximum |
Einem Kegel vom Radius R und der Höhe H werden Zylinder eingeschrieben.
Welcher von diesen Zylindern hat das größte Volumen?
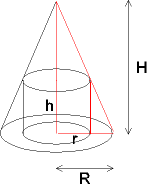
| Zielfunktion: |
V(r,h) = r²ph ® Maximum |
| Nebenbedingung: |
Die roten Dreiecke sind ähnlich:
H : R = h : (R-r)
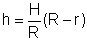 |
| einsetzen: |
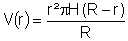 |
| vereinfachen: |
V~(r) = r²(R-r) = Rr² - r³ |
| differenzieren: |
V~'(r) = 2Rr - 3r²
V~''(r) = 2R - 6r |
| Maximum berechnen: |
2Rr - 3r² = 0
r1 = 0, r2 = 2R/3 |
| Kontrolle: |
V~''(0) = 2R > 0 Þ Minimum
V~''(2R/3) = -2R < 0 Þ Maximum
r = 2R/3, h = H/3 |
Links:
http://www.mathe-online.at/mathint/anwdiff/i.html#Extremwertaufgaben:
ausführliche Erklärung
http://www.mathe-online.at/mathint/anwdiff/i_ExtrAufg.html: ein Beispiel
http://www.mathe-online.at/mathint/anwdiff/i_verstehen.html: etwas komplizierteres Beispiel
http://www.mathe-online.at/galerie/anwdiff/anwdiff.html#es: Applet "Schema einer Extremwertaufgabe"
http://www.mathe-online.at/materialien/matroid/files/ex/ex.html: ausführliche Erklärung mit vielen
Beispielen
Übungen
Zum Inhaltsverzeichnis