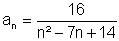
Wenn von einer Folge einige Glieder gegeben sind, kann man das Bildungsgesetz nicht eindeutig bestimmen - es gibt immer unendlich viele Möglichkeiten!
Die Folge <2, 4, 8, ... > kann zum Beispiel auf folgende Arten fortgesetzt werden:
| Bildungsgesetz | |
| <2, 4, 8, 16, 32, 64, ... > | an = 2n |
| <2, 4, 8, 14, 22, 32, ... > | an = nē - n + 2 |
| <2, 4, 8, 8, 4, 2, ... > | 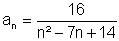 |
| <2, 4, 8, 0, 0, 0, ... > | a1 = 2, a2 = 4, a3 = 8, an = 0 für alle n > 3 |
Eine sinnvolle Aufgabe kann daher nur sein, ein möglichst einfaches Bildungsgesetz zu finden - aber auch darüber, was möglichst einfach ist, kann man streiten.