Übungen: Folgen und Reihen

Eigenschaften von Folgen

  1. Berechne die ersten fünf Glieder der angegebenen Folgen und untersuche, ob sie monoton sind:

    1. an = 5n - 3
    2. an = 20 - 2n
    3. an = n² - 6n
    4. an = n³ - n²
    5. an = 1/2n
    6. an = (-1)n/n
    7. an = (3n + 1)/2n
    8. an = 1/(n² + 1)

  2. Untersuche, ob die Folgen aus Beispiel 1 beschränkt sind. Gib, wenn möglich, je eine obere und untere Schranke an.

  3. Untersuche, ob die Folgen aus Beispiel 1 konvergent sind. Wenn ja, gib den Grenzwert an.

    4. Ergebnisse

Arithmetische Folgen und Reihen

  1. Eine Leiter hat 9 Sprossen in gleichmäßigen Abständen. Die erste Sprosse ist 30 cm hoch, die letzte 2,10 m. Berechne die Höhe der anderen Sprossen!

  2. Eine Maschine hat einen Neuwert von 60000 €. Nach 5 Jahren beträgt der Wert bei linearer Abschreibung (d.h. jedes Jahr wird derselbe Betrag abgeschrieben) nur noch 35000 €.

    1. Gib den Wert nach 1, 2, 3, 4 Jahren an. (Tipp: Bezeichne den Neuwert mit a0.)
    2. Nach wieviel Jahren ist die Maschine ganz abgeschrieben?

  3. Ein Sportler bereitet sich auf einen Marathonlauf vor. Am ersten Tag läuft er 5000 m. Er hat vor, drei Wochen lang seine Leistung täglich um 500 m zu steigern.

    1. Wie weit läuft er am 21. Tag?
    2. Welche Strecke legt er in den drei Wochen insgesamt zurück?

  4. Bei einem Wettbewerb werden 10 Preise vergeben. Der 1. Preis beträgt 1500 €, jeder weitere Preisträger erhält um 100 € weniger als der vorige.

    1. Wie hoch ist der 10. Preis?
    2. Berechne die Summe aller Preise.

    5. Ergebnisse

Geometrische Folgen und Reihen

  1. Sterne werden nach ihrer scheinbaren Helligkeit in Größenklassen eingeteilt, die eine geometrische Folge bilden. Ein Stern 1. Größe ist dabei 100mal so hell wie ein Stern 6. Größe.
    Angenommen, ein Stern 6. Größe hat die Helligkeit 1. Wie hell sind dann Sterne 1., 2., 3., 4. und 5. Größe?

  2. Wenn die Frequenz eines Tons verdoppelt wird, klingt er um eine Oktav höher. Bei der gleichschwebend-temperierten Stimmung von Musikinstrumenten wird eine Oktav in 12 Halbtöne eingeteilt, deren Frequenzen eine geometrische Folge bilden. Berechne die Frequenzen aller Halbtöne zwischen a1 (440 Hz) und a2 (880 Hz)!

  3. Ein Kind baut einen Turm aus 8 Plastikwürfeln. Die Seitenlänge des 1. Würfels beträgt 12 cm, jeder weitere hat die 0,8-fache Seitenlänge des vorigen.

    1. Welche Seitenlänge hat der 8. Würfel?
    2. Welches Volumen hat der 1. bzw. 8. Würfel?
    3. Wie hoch ist der Turm?
    4. Berechne die Summe der Volumina aller 8 Würfel!

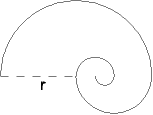
  4. An einen Halbkreis mit dem Radius r wird ein halb so großer Halbkreis angefügt, daran wieder ein halb so großer usw., so dass eine Spirale entsteht (Bild).

    1. Berechne den Grenzwert der Länge der Spirale.
    2. Wie weit ist das Zentrum der Spirale von ihrem Anfangspunkt entfernt?


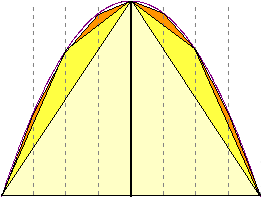
  5. Archimedes berechnete den Flächeninhalt des Parabelsegments folgendermaßen (Bild):
    Er schrieb dem Segment das größte Dreieck ein. Den Restsegmenten schrieb er wieder Dreiecke ein und zeigte, dass diese zusammen 1/4 der Fläche des ersten Dreiecks besitzen. Dieser Vorgang lässt sich beliebig oft wiederholen, wobei die Restfläche gegen 0 geht.
    Wenn das erste Dreieck den Flächeninhalt A besitzt, wie groß ist dann die Fläche des Parabelsegments?

    6. Ergebnisse


Zum Inhaltsverzeichnis