1. Stelle die folgenden Zusammenhänge als Funktionen dar!

1. Benzinpreis: 12 S/l
   x: getankte Liter, p(x): Preis
2. Telefonrechnung:
   Grundgebühr ATS 260,00
   Verbindungsentgelt ATS 9,30 pro Tarifeinheit
   x: Anzahl der Tarifeinheiten, R(x): Rechnungsbetrag
3. Taxifahrt:
   Grundgebühr ATS 28,00
   Kilometerpreis ATS 8,00
   x: gefahrene Kilometer, F(x): Fahrpreis
4. Ein Öltank enthält 500 l Heizöl. Täglicher Verbrauch: 35 l.
   t: Zeit in Tagen, R(t): restliche Ölmenge
5. Abschreibung: Eine Maschine hat einen Anschaffungswert von S 60000,- , die Nutzungsdauer beträgt 12 Jahre.
   t: Zeit in Jahren, R(t): Restwert
6. In einem quadratischen Zimmer wird ein Fussboden verlegt.
   Quadratmeterpreis: 120 S
   s: Seitenlänge des Zimmers, p(s): Preis des Fussbodens
7. s: Seitenlänge eines Holzwürfels
   r (Dichte von Holz): 0,8
   m(s): Masse des Würfels
8. Ein Betrag von 1000 S wird auf n Personen gleichmäßig aufgeteilt
   B(n): Betrag, den eine Person erhält

Gegeben sind die folgenden Funktionen über der Grundmenge R:

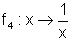
2. Zeichne die Graphen der angegebenen Funktionen im Intervall [-3, 3] mithilfe einer Wertetabelle! (Achte dabei auf die jeweilige Definitionsmenge!)
3. Ermittle die Umkehrfunktionen der gegebenen Funktionen, soweit vorhanden.
   Bsp.: f: y = x - 2     =>     f ^-1: x = y - 2     =>     y = x + 2
4. Addiere die angegebenen Funktionen!
   Bsp.: f₁(x) + f₂(x) = x + 1 + 2x = 3x + 1
1. f₁ + f₃
2. f₂ + f₃
3. f₂ + f₄
4. f₃ + f₄
5. Multipliziere die angegebenen Funktionen!
   Bsp.: f₁(x)·f₂(x) = (x + 1)·2x = 2x² + 2x
1. f_{1 ·} f₃
2. f₂ · f₃
3. f₂ · f₄
4. f₃ · f₄
6. Führe die angegebenen Funktionen hintereinander aus!
   Bsp.: f₁(f₂(x)) = 2x + 1, aber f₂(f₁(x)) = 2(x + 1) = 2x + 2
1. f₁(f₃(x))
2. f₃(f₁(x))
3. f₁(f₄(x))
4. f₄(f₁(x))
5. f₂(f₃(x))
6. f₃(f₂(x))
7. f₂(f₄(x))
8. f₄(f₂(x))

Ergebnisse

Zum Inhaltsverzeichnis