Exponential- und Logarithmusfunktionen

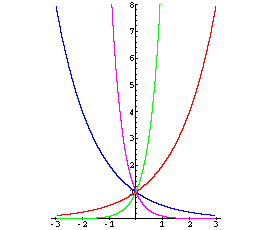
Eine Funktion der Form

f: y = ax (a > 0)

heißt Exponentialfunktion.

Ist a > 1, so wächst der Graph für positive x ins Unendliche, für negative x nähert er sich der x-Achse.
Bei a < 1 ist es umgekehrt.
Alle Graphen gehen durch den Punkt (0/1).

Graph: y = 2^x, y = 10^x, y = (1/2)^x, y = (1/10)^x

exp2: x → 2x
exp10: x → 10x
exp1/2: x → (1/2)x
exp1/10: x → (1/10)x

In der höheren Mathematik wird meist die "natürliche Exponentialfunktion" verwendet. Das ist diejenige Exponentialfunktion, deren Graph im Punkt (0/1) die Steigung 1 hat. Die Basis dieser Funktion ist die Euler'sche Zahl e = 2,71828...
(Siehe auch das Applet "Zur Definition der Eulerschen Zahl e".)

Viele natürliche Wachstumsvorgänge lassen sich durch Exponentialfunktionen beschreiben (siehe "Exponentielles Wachstum").

Die Logarithmusfunktion

y = alog x
ist die Umkehrung der Exponentialfunktion y = ax. Sie ist nur für x > 0 definiert. Die Abbildung zeigt die natürliche Exponentialfunktion und deren Umkehrung, die natürliche Logarithmusfunktion:

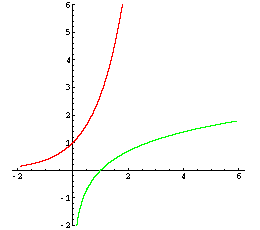
Graph: y = e^x, y = ln x

f: x → ex
f-1: x → ln x

Siehe auch: mathe online, Exponentialfunktion und Logarithmus
http://www.mathe-online.at/mathint/log/i.html

Lernziele:

  • Ich erkenne die Graphen von Exponential- und Logarithmusfunktionen.

Zum Inhaltsverzeichnis