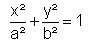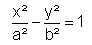Übungen: Kegelschnitte

Ellipse:

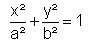
e² = a² - b²

Hyperbel:

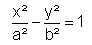
e² = a² + b²

Parabel:

y² = 2px

p = 2e

  1. Wie lauten die Gleichungen der folgenden Kegelschnitte in 1. Hauptlage? (Ohne Brüche!)
    1. ell: a = 5, b = 3
    2. ell: a = 20, b = 5
    3. ell: a = 10, e = 8
    4. ell: a = 4, e = 2√2
    5. ell: b = 5, e = 10
    6. ell: b = 10, e = 5√5
    7. hyp: a = 3, b = 4
    8. hyp: a = 5, b = 5
    9. hyp: a = 4, e = 5
    10. hyp: a = 4, e = 6
    11. hyp: b = 8, e = 10
    12. hyp: b = 3√3 , e = 9
    13. par: p = 2
    14. par: e = 3

  2. Berechne bei den folgenden Kegelschnitten die Länge der Halbachsen a und b (bzw. Parameter p) und die Brennweite e!
    1. ell: 16x² + 25y² = 400
    2. ell: x² + 4y² = 100
    3. ell: 4x² + 9y² = 324
    4. ell: 5x² + 9y² = 180
    5. hyp: x² - 9y² = 225
    6. hyp: x² - y² = 100
    7. hyp: 4x² - 9y² = 144
    8. hyp: 3x² - y² = 12
    9. par: y² = 8x
    10. par: y² = x

  3. Ermittle die Gleichungen der Kegelschnitte in 1. Hauptlage, die durch den angegebenen Punkt gehen!
    1. ell: a = 10, P(8/3)
    2. ell: a = 20, P(12/-4)
    3. ell: b = 10, P(12/6)
    4. ell: b = √2, P(-5/1)
    5. hyp: a = 10, P(15/-5)
    6. hyp: b = 15, P(10/20)
    7. hyp: a = 12, P(-15/3)
    8. hyp: b = 6, P(-10/-8)
    9. par: P(2/4)
    10. par: P(6/-3)

  4. Berechne - wenn vorhanden - die Schnittpunkte von Kegelschnitt und Gerade!
    1. ell: 5x² + 20y² = 100
      g: x - 2y = -2
    2. ell: 9x² + 4y² = 36
      g: 4x + 5y = 20
    3. ell: x² + 4y² = 2500
      g: x + y = 55
    4. ell: 9x² + 25y² = 225
      g: 4x + 5y = 25
    5. hyp: x² - y² = 9
      g: x + 2y = -3
    6. hyp: 16x² - 7y² = 81
      g: 2x - y = 3
    7. hyp: 4x² - 9y² = 144
      g: 10x - 9y = 48
    8. hyp: 16x² - 9y² = 576
      g: 4x - y = 8
    9. par: y² = 4x
      g: 2x - 5y = -12
    10. par: y² = x/4
      g: x - 2y = 6
    11. par: y² = 12x
      g: 7x - 3y = -9
    12. par: y² = 9x
      g: 4x - 4y = -9

  5. Ermittle die Gleichung der Tangente des angegebenen Kegelschnitts im Punkt T:
    1. ell: x² + 4y² = 100, T(6/y>0)
    2. ell: 3x² + 4y² = 48, T(x<0/3)
    3. ell: 9x² + 25y² = 225, T(4/y<0)
    4. hyp: x² - y² = 9, T(x>0/4)
    5. hyp: 3x² - y² = 3, T(x>0/-3)
    6. hyp: x² - 4y² = 25, T(-13/y<0)
    7. par: y² = 8x, T(2/y>0)
    8. par: y² = 3x, T(x/-6)

  6. Berechne die Halbachsen (bzw. Radius, Parameter), die Schnittpunkte und Schnittwinkel folgender Kegelschnitte:
    1. ell: x² + 9y² = 18
      k: x² + y² = 10
    2. hyp: 4x² - y² = 12
      k: x² + y² = 8
    3. hyp: x² - 4y² = 256
      ell: 4x² + 25y² = 2500
    4. ell: x² + 9y² = 225
      k: (x - 16)² + y² = 25
    5. par: y² = 2x
      hyp: 4x² - y² = 12
    6. par: y² = x
      ell: x² + 4y² = 32

Ergebnisse

Zum Inhaltsverzeichnis