|
Beispiel: Der Schnittpunkt der beiden Graphen entspricht dem Marktgleichgewicht: |
 |
Wie kommt der Marktpreis eigentlich zustande? Wir haben gesehen, dass der Produzent den maximalen Gewinn erzielt, wenn die Grenzkosten gleich dem Preis sind. Er wird also um so mehr produzieren, je höher der Preis ist, zu dem er das Produkt verkaufen kann. Die Menge, die er zu einem bestimmten Preis p anbietet, bezeichnen wir als Angebotsfunktion xa(p). Die Marktangebotsfunktion setzt sich aus den Angebotsfunktionen aller einzelnen Anbieter zusammen. Sie ist monoton wachsend (je höher der Preis, desto mehr wird angeboten).
Aus Gründen der Einheitlichkeit nimmt man die Menge x als unabhängige Variable. Man rechnet daher mit der inversen Angebotsfunktion pa(x). Das ist der Preis, zu dem eine bestimmte Menge x angeboten wird.
Ebenso erhält man aus den Nachfragefunktionen der einzelnen Konsumentinnen die Marktnachfragefunktion xn(p). Sie ist normalerweise monoton fallend (je höher der Preis, umso weniger wird verkauft). Auch hier rechnet man mit der inversen Nachfragefunktion pn(x). Das ist der Preis, zu dem eine bestimmte Menge x abgesetzt werden kann.
Das Marktgleichgewicht stellt sich ein, wenn Angebots- und Nachfragepreis gleich hoch sind.
Beispiel:
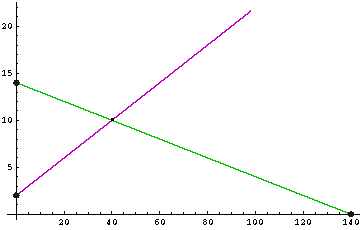
Angebotsfunktion: pa(x) = 0,2x + 2
Nachfragefunktion: pn(x) = -0,1x + 14Der Schnittpunkt der beiden Graphen entspricht dem Marktgleichgewicht:
Der Gleichgewichtspreis beträgt also
x = 40, pa(40) = pn(40) = 1010 GE; zu diesem Preis werden40 ME verkauft.
Bei der Nachfragefunktion gibt es zwei wichtige Werte:
der Höchstpreis pn(0) gibt an, ab welchem Preis nichts mehr verkauft wird;
die Sättigungsmenge ist die Menge, die höchstens abgesetzt werden kann; man erhält sie aus der
Gleichung
Im Beispiel ist der Höchstpreis 14 GE, die Sättigungsmenge beträgt 140 ME.
Ein Monopolanbieter kann für sein Produkt jeden Preis verlangen, den er will. Allerdings muss er berücksichtigen, dass bei höheren Preisen die Nachfrage abnimmt. Er sollte daher die Nachfragefunktion (die wir ab jetzt einfach mit p(x) bezeichnen) kennen.
| p(x) | (inverse) Nachfragefunktion |
| E(x) = p(x)·x | Erlösfunktion (Umsatz) |
| G(x) = E(x) - K(x) | Gewinnfunktion |
Die Gewinngrenzen und den maximalen Gewinn berechnet man so wie vorhin. Den Punkt C(x*/p(x*)) der Nachfragefunktion, bei dem der maximale Gewinn erzielt wird, bezeichnet man als Cournot'schen Punkt.
Beispiel:
Ein Monopolbetrieb hat die KostenfunktionK(x) = 0,1x² + 2x + 40.
Die Nachfragefunktion ist gegeben durchp(x) = -0,1x + 14.
Daraus erhalten wir die Gewinnfunktion:
G(x) = (-0,1x + 14)x - (0,1x² + 2x + 40) = -0,2x² + 12x - 40 Die Gewinngrenzen sind die Lösungen der Gleichung
Die GleichungE(x) = K(x) (bzw.G(x) = 0 ):x1 = 3,5, x2 = 56,5. E'(x) = K'(x) (bzw.G'(x) = 0 ) hat die Lösungx = 30. Die Firma erzielt also den maximalen Gewinn bei einem Absatz von 30 ME; sie kann einen Preis vonp(30) = 11 GE verlangen und macht dabeiG(30) = 140 GE Gewinn.
Wir sehen also, dass ein Monopolanbieter einen höheren Preis verlangen wird und dass das Angebot niedriger sein wird als auf einem freien Markt.