Kurvendiskussionen (Schritt für Schritt)

 

Wir untersuchen die Funktion f: R ® R, f(x) = x³/4 - 3x² + 9x.
Die Definitionsmenge D = R, d.h. für x können alle reellen Zahlen eingesetzt werden.

Vorbemerkung: Bitte nicht verwechseln!
f(x) ist der allgemeine Funktionswert (für beliebige x-Werte)
f(1) ist ein bestimmter Funktionswert (für x = 1)
f(x) = 0 ist eine Gleichung, die von bestimmten x-Werten erfüllt wird.

(1)

f(x) = x³/4 - 3x² + 9x

d.h., zu jedem x-Wert erhält man den zugehörigen y-Wert durch Einsetzen von x in x³/4 - 3x² + 9x
z.B. f(1) = 1³/4 - 3× 1² + 9× 1 = 6¼
Þ der Punkt P(1 / 6¼) liegt auf dem Graphen von f

(Anmerkung: Wir dürfen die Funktion nicht einfach mit 4 multiplizieren, weil wir ja sonst 4-mal so große y-Werte erhielten!)

(2)

f'(x) = 3x²/4 - 6x + 9

d.h., zu jedem x-Wert erhält man die 1. Ableitung (Steigung) durch Einsetzen von x in 3x²/4 - 6x + 9
z.B. f'(1) = 3× 1²/4 - 6× 1 + 9 = 3¾
Þ die Steigung der Tangente im Punkt P beträgt k = 3¾

(3)

f''(x) = 3x/2 - 6

d.h., zu jedem x-Wert erhält man die 2. Ableitung durch Einsetzen von x in 3x/2 - 6
z.B. f''(1) = 3× 1/2 - 6 = -4½ < 0
Þ der Graph ist im Punkt P rechtsgekrümmt

(4)

Schnittpunkte mit den Koordinatenachsen:

(4a)

Nullstellen: f(x) = 0

d.h., wir suchen die x-Werte, für die f(x) = 0 ist,
also die Lösungen der Gleichung x³/4 - 3x² + 9x = 0

(Anmerkung: Jetzt dürfen wir beide Seiten der Gleichung mit 4 multiplizieren!)

Wir erhalten die Lösungen x1 = 0, x2,3 = 6
Þ es gibt zwei Nullstellen: N1(0/0), N2(6/0)

(4b)

Schnittpunkt mit der y-Achse: x = 0

d.h., wir setzen x = 0 in f(x) ein und erhalten y = 0:
Sy(0/0) (fällt hier mit N1 zusammen)

(5)

Extremwerte: f'(x) = 0

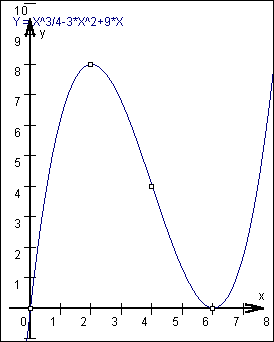
d.h., wir suchen die x-Werte, für die der Graph eine waagrechte Tangente hat (Steigung = 0), also die Lösungen der Gleichung 3x²/4 - 6x + 9 = 0

Wir erhalten die Lösungen x1 = 2, x2 = 6

Die zugehörigen y-Werte erhalten wir durch Einsetzen in f(x) (siehe (1)):
y1 = f(2) = 2³/4 - 3× 2² + 9× 2 = 8
y2 = f(6) = 6³/4 - 3× 6² + 9× 6 = 0
Þ in den Punkten E1(2/8) und E2(6/0) hat der Graph eine waagrechte Tangente.

Um die Art des Extremwertes zu bestimmen, setzen wir die x-Werte in f''(x) ein (siehe (3)):
f''(2) = 3× 2/2 - 6 = -3 < 0 Þ der Graph ist rechtsgekrümmt Þ es handelt sich um einen Hochpunkt
f''(6) = 3× 6/2 - 6 = 3 > 0 Þ der Graph ist linksgekrümmt
Þ es handelt sich um einen Tiefpunkt

Wir erhalten also als Extremwerte: H(2/8), T(6/0)

(6)

Wendepunkte: f''(x) = 0

d.h., wir suchen die x-Werte, für f''(x) = 0, also die Lösungen der Gleichung 3x/2 - 6 = 0

Wir erhalten die Lösung x = 4

Den zugehörigen y-Wert erhalten wir wieder durch Einsetzen in f(x) (siehe (1)):
f(4) = 4³/4 - 3× 4² + 9× 4 = 4
Þ es gibt einen Wendepunkt: W(4/4)

(7)

Gleichung der Tangente in einem beliebigen Punkt

Allgemeine Geradengleichung: y = kx + d
(diese Gleichung gilt für jeden Punkt der Gerade!)

z.B. Gleichung der Tangente in P(1 / 6¼):
Steigung: k = f'(1) = 3¾
Da P auf der Tangente liegt, können wir die Koordinaten von P in die Gleichung einsetzen:
6¼ = 3¾× 1 + d
Daraus können wir d berechnen: d = 2½

Die Gleichung der Tangente in P lautet also:
tP: y = 3¾ x + 2½

Die Gleichung der Wendetangente (Tangente im Wendepunkt) wird genauso ermittelt:

W(4/4), k = f'(4) = 3× 4²/4 - 6× 4 + 9 = -3
4 = -3× 4 + d Þ d = 16
tW: y = -3x + 16

Graph von f:

Zum Inhaltsverzeichnis