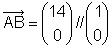
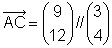
wir müssen ihn daher durch 5 dividieren:
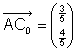
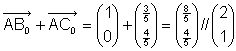
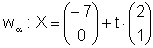
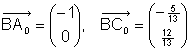
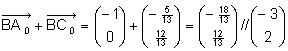
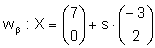
Inkreismittelpunkt:
Der Inkreismittelpunkt ist der Schnittpunkt der Winkelsymmetralen.
Man erhält einen Richtungsvektor einer Winkelsymmetralen, indem man die normierten Seitenvektoren (d.h. Vektoren vom Betrag 1) addiert.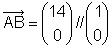 |
Dieser Vektor hat schon die Länge 1. |
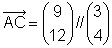 |
Dieser Vektor hat die Länge Ö(3²+4²) = 5, wir müssen ihn daher durch 5 dividieren: |
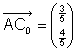 |
|
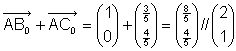 |
|
| Gleichung der Winkelsymmetralen in Parameterform: | 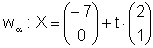 |
| parameterfrei machen: | wa: x - 2y = -7 |
| Ebenso berechnen wir wb (Richtung beachten!): | |
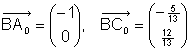 |
|
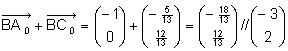 |
|
| Gleichung in Parameterform: | 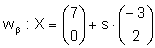 |
| parameterfrei machen: | wb: 2x + 3y = 14 |
| Schnittpunkt von wa und wb berechnen: | x = 1, y = 4 |