Rechnen mit negativen Zahlen
Weil sich innerhalb der natürlichen Zahlen nicht alle Subtraktionen ausführen lassen (z.B. 3 - 5), erweitert man den Zahlenraum um die negativen Zahlen. Das kann man sich schön mit Hilfe der Zahlengeraden veranschaulichen:
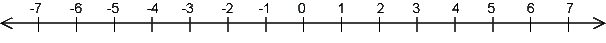
Je größer eine Zahl ist, umso weiter rechts liegt sie auf der Zahlengeraden.
Der Abstand einer Zahl vom Nullpunkt heißt Betrag (oder Absolutbetrag). Er ist immer positiv.
Zahlen, die denselben Betrag, aber entgegengesetztes Vorzeichen haben (wie +3 und -3), nennt man Gegenzahlen
Addition und Subtraktion
Beim Addieren einer positiven Zahl geht man auf der Zahlengeraden nach rechts, beim Addieren einer negativen Zahl nach links.
Eine Zahl wird subtrahiert, indem man ihre Gegenzahl addiert. Das ergibt folgende Rechenregeln:
|
+(+a) = -(-a) = +a +(-a) = -(+a) = -a |
Multiplikation und Division
Multipliziert man eine Zahl mit einer negativen Zahl so ändert sich ihr Vorzeichen. Daher ergeben sich folgende Rechenregeln:
|
(+a)·(+b) = (-a)·(-b) = +ab (+a)·(-b) = (-a)·(+b) = -ab |
Die Regeln für die Division sind ganz analog.
Potenzieren
|
(-a)n = |
ì
an, wenn n gerade |
Der Betrag einer Zahl
ist immer positiv, z.B.: |+3| = |-3| = 3
Betragsstriche ersetzen eine Klammer!
Beispiel: |(+3)+(-8)|·(-2) = |-5|·(-2) = 5·(-2) = -10