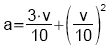Quadratische Funktionen - Übungen

  1. Zeichne die Graphen der folgenden Funktionen im angegebenen Intervall mithilfe einer Wertetabelle und berechne die Nullstellen:

    1. f(x) = x² - 2            [-2; 2]
    2. f(x) = x² - 4x            [-1; 5]
    3. f(x) = 2x² - 2x - 4       [-2; 3]
    4. f(x) = x²/2 + 2x + 2       [-5; 1]
    5. f(x) = -x² + x + 1       [-2; 3]
    6. f(x) = -2x² - 3x -2       [-3; 1]

  2. (*) Berechne bei den folgenden Parabeln die Koordinaten des Scheitels, die Schnittpunkte mit der x-Achse und skizziere die Parabeln!

    1. y = x² - 6x + 11
    2. y = x² - 2x - 3
    3. y = x² + 4x + 3
    4. y = x² + 5x + 7

  3. Berechne die Gleichung der quadratischen Funktion, deren Graph durch drei gegebene Punkte geht! Zeichne den Graph und berechne die Nullstellen!

    1. A(0/6), B(1/3), C(2/2)
    2. A(0/0), B(2/4), C(3/3)
    3. P(-1/-4), Q(1/2), R(2/11)
    4. P(1/4,5), Q(2/5), R(4/3)

  4. Die Faustregel für die Berechnung des Anhaltewegs (Fahrschulformel) lautet

    (v: Geschwindigkeit in km/h, a: Anhalteweg in m).

    1. Erstelle eine Wertetabelle für v = 0, 10, 20, ... 100 km/h und zeichne den Graphen der Funktion!
    2. Wie schnell darf man höchstens fahren, wenn der Anhalteweg 100 m betragen darf?

  5. Der Benzinverbrauch eines Autos wächst quadratisch mit der Geschwindigkeit. Bei einer bestimmten Fahrzeugtype wurden im höchsten Gang folgende Werte gemessen (v: Geschwindigkeit in km/h, B(v): Benzinverbrauch in l/100 km):

    v B(v)
    60 5,0
    80 5,8
    100 7,4

    Ermittle die Gleichung der quadratischen Funktion B(v). Wieviel Benzin verbraucht das Auto bei einer Geschwindigkeit von 130 km/h?

Ergebnisse

Zum Inhaltsverzeichnis