Trigonometrie: Vermessungsaufgaben und andere Anwendungen

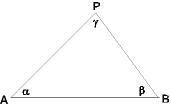
    Entfernungsbestimmung mit Horizontalwinkeln

  1. Um einen Neupunkt P zu vermessen, steckt man eine Standlinie AB ab und misst zwei der Horizontalwinkel ∠BAP = α, ∠ABP = β und ∠APB = γ. Wie weit ist der Punkt P von A bzw. B entfernt?

    1. AB = 56 m, α = 67,5°, β = 54,2°
    2. AB = 92 m, α = 42,9°, β = 113,4°
    3. AB = 135 m, α = 36,9°, γ = 95,3°
    4. AB = 64 m, β = 81,4°, γ = 21,3°


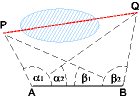
    Entfernungsbestimmung mit Horizontalwinkeln

  2. Um die nicht direkt messbare Entfernung zweier Punkte P und Q in der Ebene zu bestimmen, steckt man eine Standlinie AB ab und misst folgende Horizontalwinkel:
    ∠BAP = α1, ∠BAQ = α2, ∠ABP = β1, ∠ABQ = β2
    Wie lang ist die Strecke PQ?


    1. AB = 250 m, α1 = 102,5°, α2 = 21,6°, β1 = 37,8°, β2 = 122,3°
    2. AB = 250 m, α1 = 75,2°, α2 = 37,9°, β1 = 32,5°, β2 = 106,3°
    3. AB = 400 m, α1 = 87,2°, α2 = 63,4°, β1 = 52,1°, β2 = 79,9°

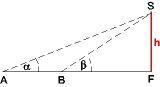
    Höhenmessung mit horizontaler Standlinie

  3. Ein alter Turm steht in einer Ebene. Um seine Höhe zu bestimmen, steckt man in der Ebene eine horizontale Standlinie AB ab, so dass A, B und der Fußpunkt des Turms in einer Linie liegen. Von A aus misst man zur Turmspitze den Höhenwinkel α, von B aus den Höhenwinkel β. Wie hoch ist der Turm, und wie weit ist sein Fußpunkt von B entfernt?


    1. AB = 100 m, α = 15,8°, β = 38,1°
    2. AB = 80 m, α = 16,9°, β = 25,3°
    3. AB = 120 m, α = 11,8°, β = 18,6°

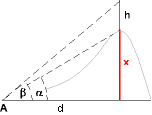
    Berg mit Mast

  4. Auf einem Berggipfel steht ein h m hoher Sendemast. Von einem Ort A im Tal sieht man den Fußpunkt des Mastes unter dem Höhenwinkel α , die Spitze unter dem Höhenwinkel β. Wie hoch ist der Berg? Berechne auch die horizontale Distanz d zwischen A und dem Berggipfel.


    1. h = 75 m, α = 17,7°, β = 24,3°
    2. h = 50 m, α = 41,6°, β = 47,3°
    3. h = 40 m, α = 31,0°, β = 34,2°

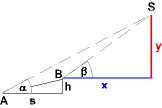
    Höhenmessung mit vertikalem Hilfsdreieck

  5. Ein Kirchturm wird von zwei Punkten A und B aus vermessen. B liegt zwischen A und dem Turm, aber um h Meter höher als A. Man misst die horizontale Distanz s von A und B sowie die Höhenwinkel α und β zur Turmspitze. Berechne den Höhenunterschied und die horizontale Entfernung zwischen B und der Turmspitze!


    1. s = 80 m, h = 4,7 m, α = 11,4°, β = 16,3°
    2. s = 114,3 m, h = 8,5 m, α = 10,2°, β = 19,7°
    3. s = 55 m, h = 2 m, α = 16,5°, β = 23,9°

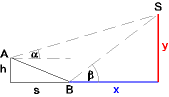
    Höhenmessung mit vertikalem Hilfsdreieck

  6. Wie Beispiel 5, aber b liegt um h Meter tiefer als A:

    1. s = 75 m, h = 3,5 m, α = 7,8°, β = 13,3°
    2. s = 62,5 m, h = 1,8 m, α = 14,0°, β = 31,7°
    3. s = 240 m, h = 12 m, α = 7,7°, β = 12,1°


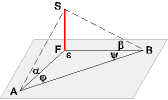
    Höhenmessung mit horizontalem Hilfsdreieck

  7. Ein Mast steht auf einer waagrechten Ebene. In der Ebene wird eine Standlinie AB abgesteckt, die mit dem Fußpunkt F des Mastes ein Dreieck bildet. Man misst die Horizontalwinkel ∠BAF = φ, ∠ABF = ψ und den Höhenwinkel α von A zur Mastspitze. Wie hoch ist der Mast?


    1. AB = 50 m, φ = 62,2°, ψ = 47,0°, α = 37,5°
    2. AB = 80 m, φ = 72,8°, ψ = 38,4°, α = 28,3°
    3. AB = 60 m, φ = 105,3°, ψ = 41,6°, α = 23,7°

  8. Von der Spitze eines h m hohen Turmes sieht man den Geländepunkt A unter dem Tiefenwinkel α, und nach Schwenken des Messgeräts um den Horizontalwinkel ε den Geländepunkt B unter dem Tiefenwinkel β. Berechne die Entfernung AB! (Skizze s. Bsp. 7)

    1. h = 63,5 m, α = 24,2°, β = 29,9°, ε = 76,4°
    2. h = 46,5 m, α = 27,5°, β = 34,8°, ε = 112,2°
    3. h = 55 m, α = 14,0°, β = 12,7°, ε = 51,6°

  9. Zwei Schiffe laufen zur gleichen Zeit vom selben Hafen aus. Das eine fährt unter dem Kurswinkel 15° mit der Geschwindigkeit 60 km/h, das andere unter dem Kurswinkel 128° mit 40 km/h. Wie weit sind die beiden Schiffe nach einer halben Stunde voneinander entfernt? (Der Kurswinkel wird von der Nordrichtung aus im Uhrzeigersinn gemessen.)

  10. Die Erde ist ca. 150 Mill. km von der Sonne entfernt, der Mars 228 Mill. km. An einem bestimmten Tag beträgt der Winkelabstand zwischen Sonne und Mars, von der Erde aus gesehen, 50°. Unter welchem Winkel sieht man die Entfernung Sonne – Erde vom Mars aus? Wie weit ist der Mars von der Erde entfernt, und welchen Winkel schließen die Verbindungslinien Sonne – Erde und Sonne – Mars miteinander ein?

  11. Die Entfernung der Venus von der Sonne beträgt ca. 108 Mill. km. Rechne wie im vorigen Beispiel, wenn der Winkelabstand zwischen Sonne und Venus, von der Erde aus gesehen, 30° beträgt (2 Lösungen!). Wie groß kann der Winkelabstand Sonne – Venus höchstens sein?

    12. Die folgenden Beispiele können auch in Polarkoordinaten gerechnet werden.

  12. An einem Maschinenteil greifen zwei Kräfte F1 und F2 an, von denen Betrag und Richtungswinkel (= der Winkel, den sie mit der positiven x-Achse einschließen) gegeben sind. Berechne Betrag und Richtungswinkel der resultierenden Kraft. (Anleitung: Stelle die Kräfte als Pfeile dar. Die Resultierende ist die Diagonale des Parallelogramms, das von den beiden Pfeilen aufgespannt wird.)
    1. F1 = 80 N, α1 = 0°; F2 = 50 N, α2 = 120°
    2. F1 = 50 N, α1 = 15°; F2 = 100 N, α2 = 90°
    3. F1 = 90 N, α1 = 23°; F2 = 40 N, α2 = 108°

  13. Ein Ruderer will einen Fluss überqueren, der mit einer Geschwindigkelt von 3 km/h nach Süden fließt. Das Boot erreicht eine Eigengeschwindigkeit von 10 km/h.
    1. In welchem Winkel wird das Boot abgetrieben, wenn es einen Kurs normal zum Flussufer steuert? Mit welcher Geschwindigkeit bewegt es sich?
    2. Welchen Winkel zur Normalen muss der Ruderer einschlagen, wenn er genau gegenüber von seinem Startpunkt landen will? Mit welcher Geschwindigkeit kommt er dann vorwärts?

  14. Ein Sportflugzeug fliegt mit einer Eigengeschwindlgkeit von 200 km/h nach Osten. Der Wind weht mit 50 km/h aus Südosten.
    1. In welchem Winkel wird das Flugzeug abgetrieben, wenn der Pilot direkt nach Osten steuert? Wie hoch ist seine Geschwindigkeit über Grund?
    2. Welchen Winkel zur Ostrichtung muss der Pilot steuern, wenn er genau nach Osten fliegen will? Mit welcher Geschwindigkeit ist er dann unterwegs?

Ergebnisse

Zum Inhaltsverzeichnis