Nr. 11 / Oktober 2005

Heute beschäftigen wir uns mit der Frage: Was ist eigentlich eine Geometrie? Wir werden sehen, dass es außer der gewohnten, euklidischen Geometrie noch andere gibt, die mit unserer normalen Anschauung nicht viel zu tun haben.
Bekanntlich schrieb Euklid um 300 v.Chr. die "Elemente der Geometrie", die bis in die Neuzeit das mathematische Standardwerk waren. Er wollte die ganze Mathematik logisch aus einigen einleuchtenden Grundsätzen ableiten. Dazu stellte er an den Beginn seines Werkes fünf Postulate (heute würde man sie als Axiome bezeichnen):
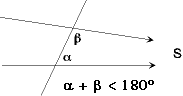
Dabei fällt das fünfte Postulat schon wegen seiner komplizierten Formulierung aus der Reihe. Wie man zeigen kann, ist es äquivalent zu folgender Aussage:
Man bezeichnet es daher als "Parallelenpostulat". Jahrhundertelang haben viele Mathematiker versucht, diese Behauptung aus den übrigen Axiomen abzuleiten. In diesem Fall wäre sie kein Axiom, sondern ein beweisbarer Satz. Sie hatten aber keinen Erfolg.
Der Jesuit Girolamo Saccheri (1677 - 1733) veröffentlichte eine Schrift mit dem Titel "Euklid, von jedem Makel gereinigt". Darin untersuchte er ein Viereck, das bei A und B rechte Winkel hat und bei dem die Seiten AD und BC gleich lang sind. In der euklidischen Geometrie ist das ein Rechteck. Ohne das fünfte Postulat kann man nur zeigen, dass die Winkel bei C und D gleich groß sind. Sie könnten aber beide spitz oder beide stumpf sein. Saccheri untersuchte nun die "Hypothese des spitzen Winkels" und die die "Hypothese des stumpfen Winkels" so weit, bis er auf Ergebnisse kam, die ihm unsinnig vorkamen. Damit meinte er, das Parallelenpostulat bewiesen zu haben.

Erst in der ersten Hälfte des 19. Jahrhunderts kamen einige Mathematiker undabhängig voneinander auf die Idee, an das Problem ganz anders heranzugehen. Es waren Carl Friedrich Gauß (1777 - 1855), Janos von Bolyai (1802 - 1860) und Nikolai Iwanowitsch Lobatschewski (1793 - 1865). Ihre Idee war: Wir lassen das fünfte Postulat weg und schauen, wie weit wir kommen. Dabei verzichten wir auf die Anschauung und beschränken uns nur auf die Sätze, die wir aus den ersten vier Postulaten logisch ableiten können. Zu ihrer Überraschung ergab sich aus der Annahme, dass es mehrere Parallelen gäbe, eine zwar ungewohnte, aber in sich widerspruchsfreie Geometrie - die "nichteuklidische Geometrie".
Bernhard Riemann (1826 - 1866) fand später auch eine Geometrie, in der es gar keine Parallelen gibt. Aus Gründen, die hier nicht erklärt werden können, nannte Felix Klein (1849 - 1926) diese beiden Typen von nichteuklidischen Geometrien "hyperbolische" und "elliptische" Geometrie.
Damit war gezeigt, dass das Parallelenaxiom wirklich von den anderen Axiomen unabhängig ist. Nun fragte man sich, welche Geometrie die "richtige" ist, das heißt, welche die physikalische Realität am besten beschreibt. Erst um die Jahrhundertwende setzte sich die Auffassung durch, dass es gar nicht die Aufgabe der Mathematik ist, die Wirklichkeit zu beschreiben. Ob eine mathematische Theorie "richtig" ist, lässt sich nur danach beurteilen, ob sie logisch korrekt aus den zugrundegelegten Axiomen abgeleitet ist und keine inneren Widersprüche enthält. (Das schließt natürlich nicht aus, dass die Mathematik brauchbare Modelle der Wirklichkeit liefern kann. Das ist aber Sache der Anwendungswissenschaften, wie Physik, Statistik, Wirtschaftswissenschaften ...)
In diesem Sinn schrieb David Hilbert (1862 - 1943) seine "Grundlagen der Geometrie" (1899). Er begann:
"Wir denken drei verschiedene Systeme von Dingen:
die Dinge des ersten Systems nennen wir Punkte und bezeichnen sie mit A, B, C, ... ;
die Dinge des zweiten Systems nennen wir Geraden und bezeichnen sie mit a, b, c, ... ;
die Dinge des dritten Systems nennen wir Ebenen und bezeichnen sie mit α, β, γ, ... .
Wir denken die Punkte, Geraden, Ebenen in gewissen gegenseitigen Beziehungen und bezeichnen diese Beziehungen durch Worte wie 'liegen', 'zwischen', 'kongruent', 'parallel', 'stetig'; die genaue und für die mathematische Zwecke vollständige Beschreibung dieser Beziehungen erfolgt aus den Axiomen der Geometrie."
Nach dieser Auffassung ist es völlig egal, was man sich unter diesen Objekten vorstellt. Hilbert sagte einmal: "Man muss jederzeit statt 'Punkte, Geraden, Ebenen' 'Tische, Stühle, Bierseidel' sagen können." (Das Gespräch fand in einer Bahnhofswirtschaft statt.)
Natürlich braucht der Mensch konkrete Vorstellungen. Daher wurden im Lauf der Zeit verschiedene Modelle für die nichteuklidische(n) Geometrie(n) entwickelt. Dabei ist es aber wichtig, das Modell nicht mit der Wirklichkeit zu verwechseln. So können die "Geraden" in einem Modell ganz anders aussehen als das, was wir uns normalerweise unter einer Geraden vorstellen. Wir werden jetzt die verschiedenen Geometrien vergleichen und einige Modelle kennenlernen.
Das ist unsere gewohnte Geometrie, in der das Parallelenpostulat gilt. Modell ist ein normales Zeichenblatt :-) In ihr gibt es Sätze wie:
Für diese Geometrie gibt es ein sehr anschauliches Modell: die Oberfläche einer Kugel. Die "Geraden" sind in diesem Modell die Großkreise. Es gibt also keine Parallelen. Allerdings schneiden einander zwei Großkreise immer in zwei Punkten. Dieses Problem können wir umgehen, indem wir jeweils zwei gegenüberliegende Kugelpunkte identifizieren (als einen betrachten). Ein "Punkt" ist also ein Paar von zwei gegenüberliegenden Punkten. Wir können auch nur eine Halbkugel, zum Beispiel die südliche, betrachten. Am Äquator müssen wir allerdings auch gegenüberliegende Punkte identifizieren.
Wir können die Kugelpunkte aus dem Mittelpunkt auf eine Ebene projizieren (siehe http://www1.kcn.ne.jp/~iittoo/use1_paral.htm). Die Großkreise werden dabei auf Geraden abgebildet. Nur das Bild des Äquators liegt im Unendlichen - wir müssen also die "Ferngerade" zu unserem Modell dazunehmen und erhalten so die projektive Ebene (darüber ein anderes Mal mehr). Allerdings werden Längen und Winkel nicht in ihrer wahren Größe abgebildet.
Wenn wir ein ebenes, winkeltreues Modell wollen, können wir die stereographische Projektion zu Hilfe nehmen (siehe letzter Newsletter). Die Südhalbkugel wird dabei auf das Innere eines Kreises abgebildet; die "Geraden" werden zu Kreisbögen, die den Randkreis in gegenüberliegenden Punkten schneiden.
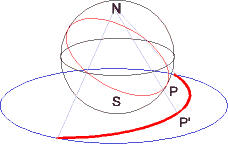
Der Randkreis ist nicht wirklich eine Grenze - man muss sich vorstellen, dass ein Punkt, der auf einer Seite den Rand erreicht, auf der anderen Seite wieder hineinkommt. Die elliptische Ebene ist also unbegrenzt, hat aber trotzdem nur einen endlichen Flächeninhalt von 2π. Eine Gerade hat die Länge π.
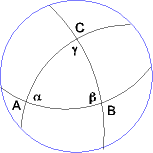
Die Winkelsumme im Dreieck ist immer größer als 180°. Man kann zeigen, dass der "Exzess" α + β + γ - 180° proportional zur Dreiecksfläche ist.
Zur Berechnung von Dreiecken auf der Kugel (und damit auch in der elliptischen Ebene) braucht man die sphärische Trigonometrie. Einige Sätze daraus:
(Man kann ja eine Strecke auf der Kugel durch den dazugehörigen Mittelpunktswinkel angeben.)
Diese Geometrie wurde noch vor der elliptischen entdeckt. Felix Klein fand dafür ein einfaches Modell: Die hyperbolische Ebene entspricht dem Inneren einer Kreisscheibe; die "Geraden" sind die Kreissehnen. Zwei "Geraden" sind parallel, wenn sie sich innerhalb der Kreisscheibe nicht schneiden.
Dieses Modell ist allerdings weder längen- noch winkeltreu. Henri Poincaré (1854 - 1912) schlug ein anderes Modell vor, in dem wenigstens die Winkel in wahrer Größe erscheinen. Auch er benutzte das Innere einer Kreisscheibe, aber die "Geraden" sind bei ihm alle Kreisbögen, die den Randkreis im einem rechten Winkel treffen.
|
|
Durch den Punkt P gehen mehrere Parallele zur Geraden g (links: Kleinsches Modell, rechts: Poincarésches Modell). In beiden Modellen gilt: Wenn man auf einer Geraden gleich große Abstände aufträgt, dann erscheinen diese im Modell immer kleiner, je näher man dem Rand kommt. Den Randkreis erreicht man auf diese Weise nie; er liegt also "in Wirklichkeit" unendlich weit entfernt. (Daher ist er strichliert gezeichnet.)
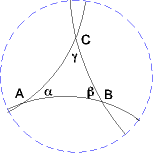
Die Winkelsumme im Dreieck ist immer kleiner als 180°. (Es gibt sogar Dreiecke, bei denen alle Winkel 0° betragen!) Der "Defekt" 180° - α - β - γ ist proportional zur Fläche des Dreiecks.
Wenn man die hyperbolische Ebene mit regelmäßigen Vielecken pflastert, erhält man phantastische Muster. Einige Beispiele findet ihr auf http://www.hadron.org/~hatch/HyperbolicTesselations/. Der holländische Maler M. C. Escher hat sich von solchen Kachelungen zu einigen seiner Bilder inspirieren lassen, z.B. Kreislimit III und Kreislimit IV.
Interessanterweise gibt es zu jedem Satz der sphärischen Trigonometrie einen entsprechenden aus der hyperbolischen Geometrie. Man muss dazu bei den Seiten die Winkelfunktionen durch die entsprechenden Hyperbelfunktionen Sinus hyperbolicus bzw. Cosinus Hyperbolicus ersetzen. so erhält man unter anderem folgende Sätze:
Übrigens kann man aus dem Kleinschen Modell das Poincarésche erhalten, indem man es senkrecht auf eine Halbkugel projiziert und von dort wieder stereograohisch auf eine Ebene (siehe http://www1.kcn.ne.jp/~iittoo/us3_poinc.htm, Bild 3 oder 3').
Wie wir vorhin gesehen haben, ist die Kugeloberfläche ein längen- und winkeltreues Modell der elliptischen Ebene. Ein entsprechendes Modell für die hyperbolische Ebene erhält man so:
|
|
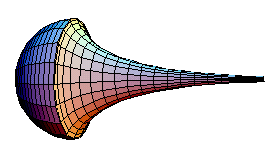
Stellen wir uns vor, ein Mann steht im Ursprung eines Koordinatensystems; sein Hund im Punkt (0/1). Das Herrchen geht jetzt auf der x-Achse nach rechts und zieht den widerstrebenden Hund hinter sich her, wobei die Leine gleich lang bleibt. Der Hund beschreibt dann eine sogenannte Traktrix (linkes Bild). Wenn diese Kurve um die x-Achse rotiert, entsteht die rechts abgebildete Fläche. Sie hat überall die Krümmung -1 und heißt daher "Pseudosphäre" (analog zur Kugel = Sphäre mit der Krümmung 1). Die geodätischen Linien auf dieser Fläche (d.h. die kürzesten Verbindungslinien zwischen zwei Punkten) entsprechen genau den Geraden der hyperbolischen Geometrie. Auf http://www1.kcn.ne.jp/~iittoo/us20_pseu.htm sieht man, wie man einen Teil der hyperbolischen Ebene auf die Pseudosphäre aufwickeln kann.
Zum Schluss möchte ich noch eine wichtige Anwendung in der Physik erwähnen. In der Relativitätstheorie betrachtet man die Zeit als vierte Dimension. Jedes Ereignis entspricht einem Punkt in der vierdimensionalen Raumzeit. Nun, das ist ziemlich unanschaulich. Aber man kann die Raumzeit auch mit einer Geometrie versehen, der sogenannten Minkowski-Geometrie. Und da stellt sich heraus, dass es sich dabei un eine nichteuklidische, genauer gesagt hyperbolische Geometrie handelt. In der speziellen Relativitätstheorie ist die Krümmung konstant; die allgemeine Relativitätstheorie befasst sich mit den Wirkungen von großen Massen, durch die die Raumzeit zusätzlich gekrümmt wird. Ein Teilchen bewegt sich dann auf einer geodätischen Linie. Mehr zu diesem Thema steht auf der Homepage von Franz Embacher: http://homepage.univie.ac.at/Franz.Embacher/SRT/Geometrie.html. Das ist wieder ein Beispiel dafür, dass eine ganz abstrakte mathematische Theorie eine unerwartete Anwendung finden kann.
Links:
http://geometrie.diefenbach.at/: Geometrieseiten des Gymnasiums GRG15 Diefenbachgasse (siehe "Geometrie der Kugel" und "Nichteuklidische Geometrie")
http://www1.kcn.ne.jp/~iittoo/index.html#chapters: eine sehr ausführliche, liebevoll gestaltete Seite über Nichteuklidische Geometrie (englisch)
http://projects.brg-schoren.ac.at/Spezialgebiete/NikolussiKerstin/SphaerischeTrigonometrie.html: Grundlagen der Sphärischen Trigonometrie (nach dem Schulbuch von Rosenberg/Ludwig)
http://www.math.ethz.ch/~knus/geometrie/2.pdf: Vorlesungsskriptum zur Sphärischen Geometrie (mit Vektorrechnung)
Viel Spaß bis zum nächsten Mal! Ich würde mich auch über Rückmeldungen freuen.
Jutta
E-mail: gut.jutta.gerhard@chello.at