Nr. 14 / Mai 2006
Vor längerer Zeit habe ich für meine Homepage einen Artikel über Mittelwerte geschrieben (http://members.chello.at/gut.jutta.gerhard/mittel.htm). Inzwischen habe ich aber noch viele interessante Informationen zu dem Thema gefunden. Die wichtigsten möchte ich hier zusammenfassen.
Was ist überhaupt ein Mittelwert? Ganz allgemein gesagt: Wenn wir zwei Zahlen a und b gegeben haben, suchen wir eine Vorschrift, die uns eine Zahl zwischen a und b liefert. Dafür gibt es natürlich viele verschiedene Möglichkeiten, deshalb hat man im Lauf der Zeit viele verschiedene Mittelwerte gefunden. Wir wollen uns im Folgenden darauf einigen, dass a und b positive Zahlen sind.
Pythagoras (ca. 500 v. Chr.) und seine Anhänger untersuchten bereits folgende Mittelwerte:
das arithmetische Mittel: 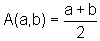
das geometrische Mittel: 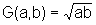
das harmonische Mittel: 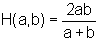 bzw.
bzw. 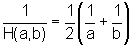
(das harmonische Mittel ist also der Kehrwert des arithmetischen Mittels der Kehrwerte von a und b).
Hier ist meine persönliche Theorie, woher die Bezeichnung "harmonisches Mittel" kommt:
Die Pythagoreer stellten auch musikalische Untersuchungen an. Wenn man eine schwingende Saite um die Hälfte verkürzt, wird der Ton um eine Oktav höher (z.B. c1 und c2). Das harmonische Mittel von 1 und 1/2 ist 2/3. Bei dieser Saitenlänge ist der Ton um eine Quint höher als der Grundton (z.B. c und g). Das harmonische Mittel von 1 und 2/3 ist 5/4 - diese Saitenlänge entspricht einer Terz (z.B. c und e). Grundton, Terz und Quint bilden einen Dur-Dreiklang, der sich sehr harmonisch anhört!
Die Pythagoreer kannten noch einige andere, nicht so prominente Mittelwerte. Das quadratische Mittel, auch "root-mean-square", wurde allerdings erst später entdeckt:
Quadratisches Mittel: 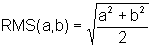
Man erhält es zum Beispiel, wenn man ein Rechteck in ein Quadrat mit gleich langer Diagonale umwandelt. Eine weitere Anwendung ist der Effektivwert von Spannungen (siehe unten).
Wenn wir mit min(a,b) die kleinere und mit max(a,b) die größere der beiden Zahlen bezeichnen, erhalten wir folgende wichtige Ungleichung:
min(a,b) ≤ H(a,b) ≤ G(a,b) ≤ A(a,b) ≤ RMS(a,b) ≤ max(a,b) (*)
Das Gleichheitszeichen gilt nur, wenn a = b. Den Beweis findet ihr auf der Homepage von Wolfgang Kirschenhofer: http://member.schule.at/kimathe/Ungleichungen.htm.
Alle diese Definitionen kann man natürlich auch auf mehr als zwei Zahlen verallgemeinern:
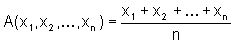
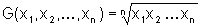
Die anderen Mittelwerte werden analog definiert. x1, x2, ..., xn sollen dabei wieder positive Zahlen sein. Auch hier gilt die Ungleichung (*).
Manchmal will man den einzelnen Werten verschiedene Gewichte zuordnen - wenn man z.B. Mittelwerte aus verschieden großen Stichproben zusammenfasst oder bei einer Prüfung der Theorie- und der Praxisteil verschieden stark in die Note eingehen sollen. Man erhält dann sogenannte gewichtete Mittel:
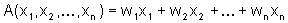
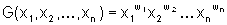
und analog für die anderen Mittelwerte. w1, w2, ..., wn sind die jeweilige Gewichte. Ihre Summe muss 1 betragen. Beim "normalen" Mittelwert sind alle Gewichte 1/n.
Beispiel: 2 Liter kochendes Wasser (100° C) werden mit 1 Liter kaltem Wasser (10° C) gemischt. Die Anteile von heißem und kaltem Wasser betragen 2/3 bzw. 1/3, die Temperatur der Mischung ist daher 2/3·100° + 1/3·10° = 70° C.
Wenn man verschieden stark gewichtete Mittelwerte vergleicht, kann man manchmal zu paradoxen Ergebnissen kommen: An einer Universität werden in allen Studiengängen prozentuell mehr Frauen als Männer zugelassen, trotzdem ist die gesamte Zulassungsquote bei den Männern höher (so geschehen in Berkeley, Kalifornien). Oder: Die Sterblichkeitsrate an Krebs hat seit 1960 in allen Altersgruppen abgenommen, trotzdem gibt es immer mehr Krebstote. Dieses Phänomen ist bekannt als Simpson's Paradox. Es wird von Walter Krämer in seinem Buch "Denkste!" ausführlich beschrieben. Eine Leseprobe findet ihr auf http://matheplanet.com/matheplanet/nuke/html/reviews.php?op=showcontent&id=70. Und hier könnt ihr selbst mit verschiedenen Zahlenwerten herumprobieren: http://www.matheprisma.uni-wuppertal.de/Module/Parad/index.htm.
(Die Lösung der beiden Beispiele: In Berkeley bewarben sich die Frauen vor allem für Fächer mit einer hohen Ablehnungsquote. Und das Krebsrisiko steigt mit dem Alter. Es gibt also deswegen immer mehr Krebstote, weil die Menschen immer älter werden.)
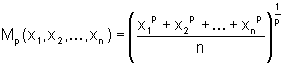
Für p = 1 erhält man das arithmetische, für p = 2 das quadratische und für p = -1 das harmonische Mittel. Wenn man p gegen 0 gehen lässt, erhält man als Grenzwert das geometrische Mittel (Beweis: http://groups.google.de/group/de.sci.mathematik/msg/f34c4257299bbf6d?hl=de&). Außerdem kann man zeigen, dass Mp umso großer wird je größer p ist. Für p → -∞ nähert sich der Mittelwert dem Minimum, für p → +∞ dem Maximum der einzelnen Werte an. Die Ungleichung (*) ist also nur ein Spezialfall dieser allgemeinen Beziehung.
Wenn wir die Durchschnittstemperatur im Lauf eines Tages bestimmen wollen, werden wir in regelmäßigen Abständen die Temperatur messen und aus den erhaltenen Werten das arithmetische Mittel bilden. Will man ein genaueres Ergebnis, so wird man mehr Messungen machen. Wenn man ständig misst, wird aus der Summe ein Integral. Wir können uns also vorstellen, dass wir die Fläche unter der Temperaturkurve durch ein flächengleiches Rechteck mit derselben Breite ersetzen. Die Höhe dieses Rechtecks ist dann die Durchschnittstemperatur. Allgemein definiert man den Mittelwert einer Funktion in einem Intervall [a, b] so:
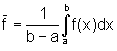
Für die anderen Mittelwerte kann man analoge Definitionen finden. Besonders wichtig ist das quadratische Mittel:
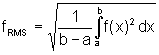
Mit dieser Formel berechnen die Physiker den Effektivwert einer Wechselspannung (d.h. die Spannung des Gleichstroms, der die gleiche Leistung liefern würde).
Die Berechnung von Quadratwurzeln nach Heron
Wie man leicht nachrechnet, gilt folgende Gleichung: G(a,b) = √A(a,b)·H(a,b). Das geometrische Mittel zweier Zahlen ist also gleichzeitig das geometrische Mittel von A und H. Wir können also √a (das geometrische Mittel von a und 1) nur mit Hilfe von Grundrechnungsarten auf folgende Weise berechnen: Wir gehen aus von den Zahlen a und 1 und bilden arithmetisches und harmonisches Mittel. Von diesen beiden Zahlen bilden wir wieder arithmetisches und harmonisches Mittel usw. Wir erhalten zwei Zahlenfolgen, die beide als Grenzwert das geometrische Mittel haben. In Formeln ausgedrückt:
a0 = a b0 = 1 an+1 = A(an, bn) bn+1 = H(an, bn)
Man bezeichnet daher das geometrische Mittel auch als arithmetisch-harmonisches Mittel. Ein Beispiel zur Berechnung von √2:
ai bi 2 1 1,5 1,3333 1,4167 1,4118 1,4142 1,4142
Nach drei Schritten hat man also schon vier richtige Dezimalstellen, und ihre Anzahl verdoppelt sich bei jedem Schritt. Diese Methode entspricht im Wesentlichen dem nach Heron von Alexandria (1. Jh. n.Chr.) benannten Verfahren, mit dem schon die Babylonier Quadratwurzeln berechnet haben. Es ist ein Spezialfall des Newton'schen Näherungsverfahrens.
Die Berechnung von Pi nach Archimedes und Gregory
Archimedes (287 - 212 v. Chr.) berechnete als erster systematisch das Verhältnis zwischen Umfang und Durchmesser eines Kreises. Er schätzte den Kreisumfang durch die Umfänge von um- und eingeschriebenen Vielecken ab, deren Eckenzahl er in jedem Schritt verdoppelte. Dabei kam er bis zum 96-Eck und fand die bekannte Abschätzung 310/71 < π < 31/7.
Der schottische Mathematiker James Gregory (1638 - 1675) verbesserte diese Methode noch, indem er folgende elegante Beziehung fand (an ist der Umfang des umschriebenen, bn des eingeschriebenen n-Ecks):
a2n = H(an, bn) b2n = G(a2n, bn)
Jede Zahl dieser Folge ist also abwechselnd das harmonische und das geometrische Mittel ihrer beiden Vorgänger. (Beachte, dass in der zweiten Formel a2n steht!) Den Beweis kann man hier nachlesen: http://mo.mathematik.uni-stuttgart.de/inhalt/erlaeuterung/erlaeuterung5/. (Gregory hat eigentlich die Flächeninhalte der Vielecke berechnet, aber dabei erhält man ganz ähnliche Formeln.)
Wenn wir von einem Kreis mit Durchmesser 1 ausgehen und mit Sechsecken beginnen (d.h. a6 = 2√3, b6 = 3), erhalten wir folgende Näherungswerte:
ai bi 3,4641 3 3,2154 3,1058 3,1597 3,1326 3,1461 3,1394 3,1427 3,1410
Wie man sieht, konvergiert das Verfahren ziemlich langsam - man erhält ungefähr alle fünf Schritte drei neue Dezimalstellen. Christiaan Huygens (1629 - 1695) fand eine weitere Verbesserung. Er bildete von an und bn noch einmal das harmonische und geometrische Mittel, aber diesmal gewichtet im Verhältnis 1/3 zu 2/3:
Eine anschauliche Erklärung dafür ist, dass die eingeschriebenen Vielecke den Kreisumfang doppelt so gut annähern wie die umschriebenen. Huygens begründete sein Verfahren mit trigonometrischen Überlegungen. Mit den Zahlen von vorhin liefert es folgende Näherungswerte:
Ai Bi 3,1402 3,1473 3,1415 3,1419 3,1416 3,1416
Wir erhalten also schon im ersten Schritt zwei richtige Dezimalstellen (eine Genauigkeit, die Archimedes erst mit dem 96-Eck erreichte) und im dritten Schritt vier - eine wesentliche Verbesserung.
Die Berechnung von Pi nach Brent und Salamin
So wie wir vorhin das arithmetisch-harmonische Mittel eingeführt haben, können wir auch das arithmetisch-geometrische Mittel definieren: Wir gehen von zwei Ausgangszahlen a und b aus, berechnen das arithmetische und geometrische Mittel, dann das arithmetische und geometrische Mittel der beiden neuen Zahlen usw. Auch diese beiden Folgen haben einen gemeinsamen Grenzwert, aber er ist nicht so einfach zu bestimmen. Carl Friedrich Gauß (1777 - 1855) stieß auf diesen Wert, als er elliptische Integrale untersuchte. (Solche Integrale treten z.B. auf, wenn man den Umfang einer Ellipse sucht; sie können nur näherungsweise berechnet werden.)
Eugène Salamin und Richard Brent gingen von Gauß' Ergebnissen aus und fanden einen Algorithmus zur Berechnung von π, den sie 1976 veröffentlichten:
a0 = 1 b0 = 1/√2 s0 = 1/2 an = A(an-1,bn-1) bn = G(an-1,bn-1) cn = an² - bn² sn = sn-1 - 2ncn pn = 2an²/sn
an und bn nähern sich dem arithmetisch-geometrischen Mittel von a und b; pn konvergiert gegen π. (Der ziemlich anspruchsvolle Beweis findet sich z.B. auf http://math-www.uni-paderborn.de/~aggathen/vorl/2004ws/sem/markus-steinborn.pdf.) Die ersten Näherungswerte lauten
p1 = 3,18767
p2 = 3,14168
p3 = 3,141592653
Im dritten Schritt erhält man also bereits neun richtige Dezimalstellen, und ihre Anzahl verdoppelt sich bei jedem weiteren Schritt! Diese Methode ist also viel besser geeignet, wenn man viele Stellen von π berechnen will. (Inzwischen haben allerdings die Brüder Borwein einige noch schnellere Algorithmen gefunden.)
Artikel "Mittelwerte" bei Wikipedia: http://de.wikipedia.org/wiki/Mittelwert
Artikel "Mean" bei MathWorld (englisch): http://mathworld.wolfram.com/Mean.html
Krämer, Walter: Denkste! Trugschlüsse aus der Welt des Zufalls und der Zahlen, Frankfurt 1995
Dalahaye, Jean-Paul: Pi - Die Story, Basel 1999
Freunde der Zahl Pi: http://www.pi314.at/
Viel Spaß bis zum nächsten Mal!
Jutta
E-mail: gut.jutta.gerhard@chello.at