Mittelwerte

Das arithmetische Mittel (meist als "Durchschnitt" bezeichnet) kennt jeder - aber habt ihr gewußt, dass es auch andere Mittelwerte gibt?

Das arithmetische Mittel

• Ein praktisches Beispiel: Peter besitzt 30 €, Paul 60 €.Wieviel bekommt jeder, wenn sie ihr gesamtes Geld gleichmäßig aufteilen?
  Die Antwort ist leicht: m = (30 + 60)/2 = 45 €.
• Definition: Das arithmetische Mittel zweier Zahlen a und b ist die Zahl m, für die gilt:
  m - a = b - m
  d.h. m ist von a und b gleichweit entfernt.

  

• Formel:
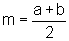
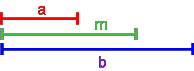
• Geometrische Konstruktion: Eine Strecke ist zu halbieren
  (entweder die Strecke a + b oder, wenn man a und b auf der Zahlengeraden aufträgt, die Strecke b - a)

  

• In einer arithmetischen Folge (z.B. 2, 4, 6, 8, 10 ...) ist jede Zahl das arithmetische Mittel ihrer beiden Nachbarzahlen.

Das geometrische Mittel

• Ein praktisches Beispiel: Ein Kapital wird ein Jahr lang mit 30%, im nächsten Jahr mit 60% verzinst. Wie hoch ist die durchschnittliche Verzinsung?
  Hier dürfen wir nicht einfach addieren - es gilt ja
  K₂ = K₀ × 1,3 × 1,6
  Wir müssen also rechnen: 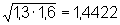, die durchschnittliche Verzinsung beträgt also 44,22%.
• Definition: Das geometrische Mittel zweier Zahlen a und b ist die Zahl g, für die gilt:
  a : g = g : b
• Formel:
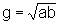
• Geometrische Konstruktion: Wir müssen ein Quadrat finden, das denselben Flächeninhalt wie das Rechteck mit den Seiten a und b hat. Das kann man z.B. mit Hilfe des Höhensatzes konstruieren:

  

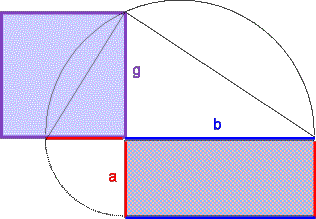
• In einer geometrischen Folge (z.B. 1, 2, 4, 8, 16 ...) ist jede Zahl das geometrische Mittel ihrer Nachbarzahlen.

Das harmonische Mittel

• Ein praktisches Beispiel: Ein Autofahrer legt 60 km mit 30 km/h, die nächsten 60 km mit 60 km/h zurück. Wie hoch war die Durchschnittsgeschwindigkeit?
  Auch hier dürfen wir nicht einfach addieren. Wir überlegen uns: Der Autofahrer hat für die ersten 60 km 2 h, für die zweiten 60 km eine Stunde gebraucht, insgesamt also 3 h für 120 km. Das ergibt eine Durchschnittsgeschwindigkeit von 40 km/h.
• Definition: Das harmonische Mittel zweier Zahlen a und b ist die Zahl h, für die gilt:
  (h - a) : (b - h) = a : b
  d.h. die Abstände von h zu den Zahlen a und b verhalten sich so wie die ursprünglichen Zahlen (ist b doppelt so groß wie a, so ist h von b doppelt so weit entfernt wie von a):

  

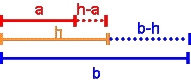
• Formel:
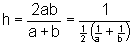
  d.h. h ist der Kehrwert des (arithmetischen) Mittels der Kehrwerte von a und b.
• Geometrische Konstruktion:
  Eine Strecke AB ist harmonisch zu teilen, d.h. der Punkt X soll die Strecke von innen im selben Verhältnis teilen wie der Punkt O von außen:
  OA : OB = XA : XB
  Das geht z.B. mit Hilfe des Strahlensatzes.
• In einer harmonischen Folge (z.B. 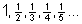) ist jede Zahl das harmonische Mittel ihrer Nachbarzahlen.

Weitere Eigenschaften

• Das Applet "Mittelwerte" zeigt, wie man m, g und h in einer Konstruktion erhalten kann. (Die Punkte O, A und B können mit der Maus verschoben werden; durch Anklicken des "Geonet"-Logos wird der ursprüngliche Zustand wiederhergestellt.)
• Es gilt immer: h £ g £ m
• g ist auch das geometrische Mittel von h und m.

↑ nach oben

¬ zurück