Nr. 7 / April 2005
Diesmal hat es etwas länger gedauert. Einerseits war ich mit meinen anderen Arbeiten etwas im Rückstand, und andrerseits habe ich mir lange überlegt, wie ich dieses nicht ganz leichte Thema angehen soll. In der Newsgroup de.sci.mathematik hat es in letzter Zeit viele Diskussionen über die Themen "Das Unendliche" und "Reelle Zahlen" gegeben. Dabei habe ich gesehen, dass sich viele Leute für diese Themen interessieren, aber keine klare Vorstellung haben, was damit gemeint ist. Daher möchte ich die historische Entwicklung und die Auffassung der heutigen Mathemaitk dazu kurz skizzieren.
Letztes Mal haben wir uns überlegt, dass man zu jeder Zahl noch eine größere finden kann - man braucht nur 1 zu addieren. Genauso kann man aber zu jeder (positiven) Zahl noch eine kleinere finden, z.B. die Hälfte der gegebenen Zahl. Die Zahlen können also nicht nur beliebig groß, sondern auch beliebig klein werden. Wir können auch eine gegebenen Strecke beliebig oft halbieren. (In der Praxis geht das natürlich nicht - wenn wir einen Gegenstand immer weiter teilen, ist spätestens auf der Ebene der Elementarteilchen Schluss. Aber in Gedanken können wir den Teilungsprozess unbegrenzt fortsetzen.) Man könnte also sagen: Eine Strecke besteht aus unendlich vielen unendlich kleinen Teilen - oder?
Der griechische Philosoph Zeno von Elea (5. Jh. v. Chr.) fand diesen Gedanken absurd. Er erfand mehrere Paradoxien, um seine Sinnlosigkeit zu beweisen. Am bekanntesten ist das Paradox von Achilles und der Schildkröte:
Der schnellste Läufer kann den langsamsten nie einholen. Denn er muss immer erst den Punkt erreichen, von dem der anderer gestartet ist. Also hat der Langsamere immer einen Vorsprung.
Stellen wir uns zum Beispiel vor, Achilles läuft mit einer Schildkröte um die Wette. Er ist zehnmal so schnell wie sie und gibt ihr ein Stadion (griechische Maßeinheit, ca. 185 m) Vorsprung. Wenn Achilles diese Strecke zurückgelegt hat, hat die Schildkröte noch 1/10 Stadion Vorsprung. Hat er auch diese Strecke hinter sich gebracht, beträgt der Vorsprung noch 1/100 Stadion und so weiter. Die Schildkröte ist also immer ein Stück voraus.
Ein anderes Mal behauptete Zeno sogar, Bewegung sei überhaupt unmöglich, denn
um eine Strecke zurückzulegen, muss man zuerst ihren Mittelpunkt erreichen. Davor muss man aber 1/4 der Strecke zurücklegen, davor 1/8 und so weiter. Die Bewegung kann überhaupt nicht beginnen, weil man vor jedem Stück unendlich viele Teilstücke durchqueren muss.
Natürlich können wir uns trotzdem bewegen, und Achilles wird die Schildkröte irgendwann einholen. Aber solche philosophischen überlegungen führten dazu, dass die griechischen Mathematiker das Wort "unendlich" nach Möglichkeit vermieden.
Archimedes (287 - 212 v. Chr.) konnte zeigen: "Der Inhalt eines Parabelsegments ist 4/3 des Inhalts des Dreiecks, das mit ihm gleiche Grundlinie und gleiche Höhe hat." Auf diese Entdeckung war er zu Recht sehr stolz. Sehen wir uns einmal an, wie er den Satz bewies:
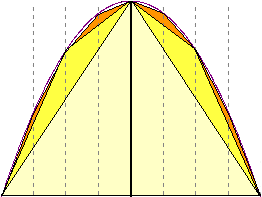Er schrieb dem Segment das größtmögliche Dreieck ein (im Bild hellgelb).
Den Restsegmenten schrieb er wieder Dreiecke ein (dunkelgelb)
und zeigte, dass diese zusammen 1/4 der Fläche des ersten Dreiecks besitzen.
Dieser Vorgang lässt sich beliebig oft wiederholen. Wenn wir also die Fläche des
ersten Dreiecks mit A bezeichnen, erhalten wir für die Summe aller Dreiecksflächen
die Reihe
In heutigen Begriffen ausgedrückt: Die Flächen der Dreiecke bilden eine geometrische Reihe
mit dem Quotienten
Eine solche Ausdrucksweise hätte Archimedes nicht akzeptiert. Er benutzte stattdessen folgenden, von den griechischen Mathematikern oft gebrauchten Satz:
Hat man zwei gleichartige Größen (z.B. zwei Flächen) und nimmt von der größeren mehr als die Hälfte weg, vom Rest wieder mehr als die Hälfte und wiederholt das immer, dann muss einmal ein Rest übrigbleiben, der kleiner als die kleinere Ausgangsgröße ist. (Nach: Euklid, Elemente X, §1)
Weil die Dreiecke in jedem Schritt größer sind als die Hälfte der übrigen Parabelstücke, wird die Restfläche - nicht "unendlich" klein, aber kleiner als jede beliebige Fläche. Ebenso verhält es sich mit der geometrischen Reihe: Nach endlich vielen Schritten ist die Summe kleiner als 4/3*A, aber die Differenz wird kleiner als jede beliebige Größe (genauer gesagt, beträgt sie immer ein Drittel des letzten Summanden). Daher kann (wie Archimedes ausführlich zeigt) die Parabelfläche nicht kleiner, aber auch nicht größer als 4/3*A sein. Also muss sie 4/3*A betragen.
Solche unendlichen Reihen begegnen uns schon, wenn wir Brüche als Dezimalzahlen schreiben wollen. Um z.B. 1/3 in eine Dezimalzahl zu verwandeln, dividieren wir 1 durch 3 und erhalten das Ergebnis 0,33333... Es wäre aber unsinnig zu sagen, 1/3 ist eine Zahl mit unendlich vielen Dezimalstellen. Denn niemand kann unendlich viele Stellen anschreiben, uns so würden wir nie 1/3 erhalten. In Wirklichkeit ist damit gemeint:
Wir haben eine unendliche Reihe, nämlich
0,3 + 0,03 + 0,003 + ...
Die Teilsummen dieser Reihe sind alle kleiner als 1/3, aber der Fehler wird immer kleiner:
| 0,3 | = 1/3 - 1/30 |
| 0,33 | = 1/3 - 1/300 |
| 0,333 | = 1/3 - 1/3000 |
Nun können wir auch das Paradoxon von Achilles und der Schildkröte auflösen, denn
die Reihe
Auch die für viele verblüffende Tatsache, dass 0,9periodisch gleich 1 ist, wird jetzt
verständlich: das ist nichts anderes der Grenzwert der Reihe
Bis jetzt haben wir nur rationale Zahlen betrachtet, also Zahlen, die als Bruch dargestellt werden können. Die griechischen Mathematiker verstanden unter "Zahl" strenggenommen nur Vielfache der Einheit, also die natürlichen Zahlen ab 2 (1 nahm als Einheit eine Sonderstellung ein). Einen Bruch betrachteten sie als Verhältnis zwischen zwei ganzen Zahlen. Das lateinische Wort ratio hat wie das griechische logos verschiedene Bedeutungen, unter anderem auch "Verhältnis"; daher kommt die Bezeichung "rationale Zahlen".
Von Pythagoras (6. Jh. v. Chr.), einem der ersten Mathematiker und Gründer einer sektenähnlichen Gemeinschaft, ist der Ausspruch überliefert: "Alles ist Zahl". Er und seine Anhänger waren der Überzeugung, alle Beziehungen in der Natur ließen sich durch Verhältnisse zwischen ganzen Zahlen ausdrücken. Es kam zu einer großen Krise, als sie entdeckten, dass es auch irrationale Verhältnisse gibt. (Hippasos, der diese Entdeckung öffentlich bekannt machte, wurde aus der Gemeinschaft ausgeschlossen und und starb später bei einem Schiffbruch. Die Pythagoreer deuteten das als Strafe der Götter, weil er Geheimnisse verraten hatte, die nur den Eingeweihten zugänglich bleiben sollten.)
Ironischerweise kann man gerade durch den Satz des Pythagoras auf irrationale
Verhältnisse stoßen. Denn für Seite und Diagonale eines Quadrats erhalten wir
Den algebraischen Beweis könnt ihr hier nachlesen:
http://www.mathe-online.at/mathint/zahlen/i_sqrt2.html.
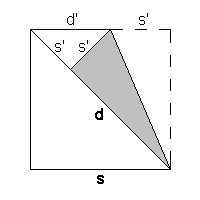
Einen geometrischen Beweis erhalten wir, wenn wir die Seite des Quadrats wie im Bild auf die
Diagonale falten. Dabei entsteht ein rechtwinkeliges Dreieck, also die Hälfte eines kleineren Quadrats mit der Seitenlänge
Der Mathematiker Eudoxos (4. Jh. v. Chr.), ein Zeitgenosse Platos, entwickelte eine Proportionenlehre, in der man auch mit irrationalen Verhältnissen mathematisch exakt rechnen konnte. Er gab einen Weg an, um festzustellen, ob ein Verhältnis gleich, kleiner oder größer als ein anderes ist. Wir können zum Beispiel sagen: Das Verhältnis d:s ist größer als 4:3, aber kleiner als 3:2. In heutiger Ausdrucksweise heißt das: 4/3 < sqrt(2) < 3/2. Mit verschiedenen Methoden (z.B. dem Heron-Verfahren, können wir diese Abschätzung beliebig verbessern. Das heißt: sqrt(2) ist keine rationale Zahl, kann aber durch rationale Zahlen angenähert werden, und zwar so, das der Fehler kleiner als jede beliebige Schranke wird. Damit sind wir wieder beim Grenzwert: sqrt(2) kann als Grenzwert einer Folge von rationalen Zahlen dargestellt werden.
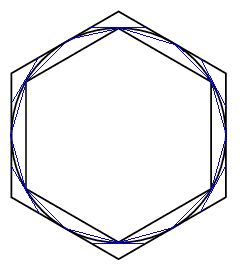Archimedes wollte auch das Verhältnis von Kreisumfang und -durchmesser,
also die Kreiszahl π berechnen. Er stellte nämlich fest, dass der Umfang eines Kreises
zwischen dem eines einbeschriebenen und eines umschriebenen Sechsecks liegen muss.
Diese Umfänge konnte er berechnen. Nun verbesserte er diese Abschätzung, indem er die
Seiten immer wieder verdoppelte, bis er beim 96-Eck angelagt war. Alle Wurzeln, die in
der Rechnung auftraten, ersetzte er durch rationale Näherungen. So gelangte er schließlich
zu dem bekannten Ergebnis: Das Verhältnis des Kreisumfangs zum Durchmesser ist kleiner als
31/7 und größer als 310/71, d.h.
Im Mittelalter gewöhnten sich die arabischen und europäischen Mathematiker immer mehr daran, mit Wurzeln zu rechnen, obwohl man nicht genau wußte, was diese Wurzeln eigentlich sind. Man bezeichnete sie auch als "numeri surdi", taube Zahlen. (Im Englischen heißt eine irrationale Quadratwurzel immer noch "quadratic surd".) Der deutsche Rechenmeister Michael Stifel (1487 - 1567) diskutierte noch, ob die irrationalen Zahlen wirkliche Zahlen oder nur fingierte sind. Er meinte aber, dass sie für die Mathematik sehr nützlich seien und man daher nicht auf sie verzichten könne. Erst René Descartes (1596 - 1650) formulierte einen neuen Zahlbegriff: Für ihn ist eine Zahl "dasjenige, was sich zur Eins verhält wie eine gerade Linie zu einer anderen geraden Linie". Seit damals versteht man unter einer reellen Zahl jede Größe, die ein Verhältnis zur Einheit hat - egal, ob ganz, gebrochen oder irrational.
Im 17. Jahrhundert bemühten sich viele Mathematiker (u.a. Kepler, Fermat und Pascal), die Flächen unter verschiedenen Kurven zu berechnen. Dabei stellten sie sich vor, dass eine solche Fläche aus unendlich vielen unendlich schmalen Streifen besteht. Damit hatten sie in vielen Fällen Erfolg. Aber die griechischen Mathematiker hätten eine solche Argumentation nicht akzeptiert.
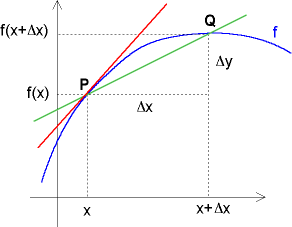Gegen Ende des 17. Jahrhunderts entdeckten Isaac Newton und Gottfried Wilhelm
Leibniz unabhängig voneinander die Differentialrechnung. Nun konnte man Tangenten an
beliebige Kurven berechnen. Leibniz betrachtete die Steigung der Sekante durch
die Punkte P und Q. Sie beträgt
Die neue Methode verbreitete sich schnell, und die Mathematiker konnten mit ihr viele Probleme lösen. Aber sie mussten sich die berechtigte Frage gefallen lassen, was denn diese "unendlich kleinen Größen" sein sollten. Waren sie Null (dann ergäbe der Ausdruck dy/dx = 0/0 keinen Sinn) oder ungleich Null (dann durfte man sie beim Grenzübergang nicht einfach weglassen)? Der englische Bischof George Berkeley nannte sie spöttisch "ghosts of departed quantities", die Geister verstorbener Größen.
Die Mathematiker des 19. Jahrhunderts bemühten sich, die Differential- und Integralrechnung auf ein logisch einwandfreies Fundament zu stellen. Die wichtigsten Beiträge leisteten dabei Bernhard Bolzano, Augustin-Louis Cauchy und Karl Weierstraß. Sie entwickelten eine exakte Definition für den Grenzwert einer Folge. Heute wird diese Definition meist so formuliert:
Die Folge <an> konvergiert gegen den Grenzwert a, wenn gilt:
Zu jedem ε > 0 gibt es eine natürliche Zahl N, so dass |an - a| < ε für alle n > N.Anders ausgedrückt: Zu jeder noch so kleine Schranke ε gibt es eine Stelle in der Folge, ab der alle Folgenglieder um weniger als ε vom Grenzwert abweichen.
So ähnlich definiert man auch den Grenzwert einer Funktion. Damit ist es nicht mehr nötig, von "unendlich kleinen" Größen zu reden - entscheidend ist nur, dass man die Abweichung zum Grenzwert beliebig klein machen kann. (Wenn man sagt "der Grenzwert für n gegen unendlich", dann ist das nur eine abgekürzte Redeweise, damit man nicht jedesmal die ganze Definition wiederholen muss! In Wirklichkeit hat man immer nur mit endliche Größen zu tun!)
Nun kann man alle Probleme, die wir angesprochen haben, auf einen einheitlichen Grenzwertbegriff zurückführen. Eine "unendliche Summe" ist der Grenzwert der Teilsummen (z.B. ist 0,333... = 0,3 + 0,03 + 0,003 + ... der Grenzwert der Folge <0,3; 0,33; 0,333; ...>). Eine reelle Zahl ist der Grenzwert der rationalen Näherungen (z.B ist sqrt(2) der Grenzwert von <1; 1,4; 1,41; 1,414; ...>). Und die Ableitung einer Funktion ist der Grenzwert von Δy/Δx, wenn Δx gegen 0 geht.
Herzliche Glückwunsch, dass ihr euch durch dieses nicht ganz einfache Thema durchgearbeitet habt, und alles Gute bis zum nächsten Mal!
Jutta
E-mail: gut.jutta.gerhard@chello.at