Kapitel3

3.3 Einführung in das Alpha-System

Durch einen Client-Server-Ansatz läßt sich die systemtechnische Entsprechung der Beziehung zwischen Teilnehmer und Administration modellieren. Wenn ein Teilnehmer interaktiv auf Entscheidungsdienste zugreift, kontrolliert der Client die Softwarekomponente, die dem Benutzer Zugang zum Wahldienst verschafft. Jeder Teilnehmer besitzt ein zertifiziertes Client-Programm und benützt die verfügbaren Dienste mittelbar durch Client. Dieser führt die Kommunikationsprotokolle aus, und präsentiert dem Nutzer ein benutzerfreundliches Interface, so daß die Stimmabgabe per Mausklick möglich wird und die teilweise komplexen Protokolle versteckt bleiben.

Eine lokale Administration besteht im Alpha-System aus dem Bulletin-Board-System (BBS) und dem Auswertungs-Server. Die Hauptkomponenten des Alpha-Systems leisten nachfolgende Aufgaben:

Client kontrolliert im Alpha-System einen geheimen Schlüssel des Wählers, dessen zugehöriger öffentlicher Schlüssel vom Trust-Center zertifiziert wurde. Das Zertifikat besteht aus einer digitalen Signatur des Trust-Centers zum öffentlichen Schlüssel des Teilnehmers.
Das Bulletin-Board-System (BBS) ist ein Rechnersystem mit unlöschbaren Speichereinheiten. Der Teilnehmer kommuniziert mit BBS über öffentliche Kanäle. Die Kommunikationsvorgänge sind öffentlich und können deswegen von jedem Beteiligten (einschließlich Außenstehenden) gelesen werden. BBS dient zur Aufzeichnung der Entscheidungsdaten, um die korrekte Ergebnisermittlung öffentlich nachvollziehbar zu machen. Kein Beteiligter ist imstande, die vom BBS dargestellten Daten zu löschen.
Will ein Teilnehmer eine Nachricht zum BBS übertragen, so authentifiziert er diesen Schreibzugriff mit seiner digitalen Signatur (Zugriffskontrolle). Aufgrund der Annahme, daß nur autorisierte Teilnehmer in das BBS schreiben dürfen, können Angriffe, die den Boykott des Dienstes (Denial of Service) zum Ziel haben, verhindert werden.
Der Auswertungs-Server evaluiert die Entscheidungsdaten und publiziert die Resultate sowie die Auswertungsliste, die alle empfangenen Entscheidungsdaten enthält, im BBS.

3.3.1 Alpha-1-System: E-Initiative

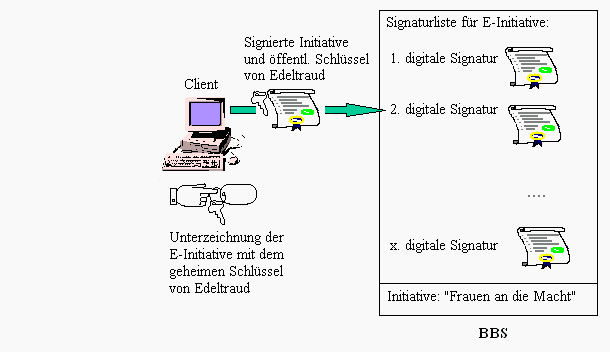
Das einfachste Protokoll wird als Alpha-1-System bezeichnet. Wenn der Wähler eine Inititative (Volksbegehren) unterstützen möchte, sendet sein Client eine digitale Signatur zum Antrag (Vorlage) über das Netz zum BBS. Da Client seinen öffentlichen Schlüssel zum BBS überträgt, ist BBS imstande, seine digitale Signatur zu verifizieren. Im BBS erscheint die Unterschriftenliste.

Abbildung 3.2: Elektronische Unterzeichnung einer E-Initiative (E-Volksbegehren).

3.3.2 Alpha-2-System: pseudonymisierte E-Initiative

Das Alpha-1-System weist ein Datenschutzdefizit auf, da die Identität des Unterzeichners für Außenstehende eindeutig identifizierbar ist. Diese Tatsache kann ggf. für manche Teilnehmer ungünstige Konsequenzen hervorrufen. Beispielsweise unterstützen Arbeitnehmer eine Initiative, die sich gegen die Unternehmenspolitik des Arbeitgebers richtet. Wenn der Arbeitgeber nachträglich den Inhalt des BBS ausliest, dann können diese Personen identifiziert werden. Das pseudonymisierte Alpha-2-System behebt derartige Probleme. Allerdings bietet das Alpha-2-System keinen Schutz der Kommunikationsumstände (wer wann mit BBS kommunizierte).

Der Client generiert zunächst ein asymmetrisches Zufallsschlüsselpaar. Mit seinem geheimen Zufallsschlüssel unterzeichnet Client den Antrag und erhält eine Pseudonym-Signatur. Seinen öffentlichen Zufallsschlüssel signiert Client mit seinem offiziellen geheimen Schlüssel. Daraufhin chiffriert Client die nachstehenden Daten mit dem öffentlichen Schlüssel des Auswertungs-Servers:

öffentlicher Schlüssel des Teilnehmers,
öffentlicher Zufallsschlüssel des Teilnehmers,
Pseudonym-Signatur zum Antrag (Vorlage),
Signatur vom Client zur Pseudonym-Signatur.

Das chiffrierte Datenpaket transferiert Client zum Auswertungs-Server. Dieser dechiffriert die Nachricht und publiziert den öffentlichen Zufallsschlüssel mit der Pseudonym-Signatur im BBS, damit der Teilnehmer nachträglich prüfen kann, ob seine Signatur gezählt wurde. Wenn die Client-Signatur korrekt ist, dann inkrementiert der Auswertungs-Server den Zählerstand.

3.3.3 Alpha-3-System: offene E-Wahlen

Das Alpha-3-System realisiert offene (nichtanonyme) E-Wahlen und E-Abstimmungen. Es erfüllt das Kriterium der Nichtbeeinflußbarkeit, indem der Schlüssel zur Dechiffrierung der Wahlscheine auf mehrere Instanzen verteilt wird. Jede RA führt in Kooperation mit den Auswertungs-Servern ihrer LAen ein Verteilungsprotokoll durch, um einen öffentlichen Kollektivschlüssel zu erzeugen und den korrespondierenden geheimen Schlüssel auf die mitwirkenden Einheiten aufzuteilen. Nach dem Ende des Protokolls besitzt jeder Protokollteilnehmer einen geheimen Teilschlüssel. Mit dem öffentlichen Kollektivschlüssel codiert Client die Wahlscheindaten und transferiert das Ergebnis zum BBS. Das Entschlüsseln der Wahlscheine ist unter der Voraussetzung eines sicheren Secret-Sharing-Schemas nur dann möglich, wenn die RA und ihre zugeordneten Auswertungs-Server

alle geheimen Teilschlüssel miteinander zusammenschließen, oder
jeweils eine Entschlüsselung der codierten Wahlscheine mit ihrem geheimen Teilschlüssel vornehmen.

Demzufolge kann niemand vor Ende der Wahlzeit Teilergebnisse entschlüsseln, solange mindestens eine Einheit ordnungsgemäß arbeitet. Eine RA und ihre untergeordneten Auswertungs-Server werden im Alpha-3-System als Dechiffrierungskreis bezeichnet.

3.3.4 Alpha-4-System: E-Losentscheid

Das klassische Athen läßt sich als Ursprung der Politik deuten. Die Verfassung von Athen beruhte auf einer direktdemokratischen Ordnung. Bereits antike Quellen stimmten hinsichtlich der Bedeutung der Repräsentantenwahl nach dem Losprinzip für die Demokratie darin überein, "daß der Losentscheid ein demokratisches Mittel ist, um Armen wie Reichen dieselben Chancen einzuräumen - ein Standpunkt, den Aristoteles in "Der Staat der Athener" uneingeschränkt unterstützt" (Barber, 1994, S. 271). Für Aristoteles muß in der Demokratie die Gleichheit am stärksten ausgeprägt sein. Weder reich noch arm dürfen eine privilegierte Position haben, sondern beide sollten ebenbürtig an der Regierung beteiligt sein.

Daran anschließend wird über 2500 Jahre später das Alpha-4-System entwickelt, das die sichere E-Repräsentantenwahl per Zufallsentscheid umsetzt. Das Realisieren eines Wahlverfahrens per Los erscheint zunächst als triviale Aufgabe, da ein einziger Rechner, der per Zufallsgenerator die betreffenden Personen aussucht, genügen würde. Damit sind der unzulässigen Manipulation am Losentscheidprogramm aber Tür und Tor geöffnet. Eine Zufallsselektion, die eine einzige Instanz durchführt, kann beliebig manipuliert werden (z.B. die Ermittlungssoftware enthält ein trojanisches Pferd, das die von der Administration erwünschten Kandidaten als Ausgabe liefert). Selbst wenn ein fälschungssicheres Modul die selektierten Kandidaten mit Signatur liefert, muß dem Gerät vertraut werden (d.h. es besitzt keine Computer-Anomalien).

Führen mehrere einander wechselseitig mißtrauende Instanzen das Protokoll zur Repräsentantenwahl aus, wobei jede Instanz zufällige Eingabewerte zur sicheren Berechnung der Repräsentanten liefert, steigert dies die Sicherheit. Kann die Sicherheit weiter erhöht werden? Die Korrektheit der Ermittlung ist auch ohne jegliches Vertrauen der Wähler gegenüber den unabhängigen Instanzen gegeben, wenn auch die Wähler daran partizipieren.

Abbildung 3.3: Übertragung der versiegelten Zufallszahlen.

Im folgenden wird ein Protokoll zur Repräsentantenwahl skizziert. Zuerst generiert Client für jede zu wählende repräsentative Position eine Zufallszahl, die dieser durch Anwendung einer öffentlichen Commitment-Funktion chiffriert. Die besondere Eigenschaft des Commitment-Schemas beruht darauf, daß der Sender (Client) eine Nachricht codiert, die vom Empfänger nur dann entschlüsselbar ist, wenn der Sender eine zusätzliche Information (Commitment-Schlüssel) preisgibt. Außerdem wird für den Außenstehenden sichergestellt, daß sowohl Sender als auch Empfänger die Nachricht später nicht verändern können, weil die Eindeutigkeit der Öffnung des Commitments garantiert wird. Zunächst hält Client die Commitment-Schlüssel geheim. Die damit codierten (versiegelten) Zufallszahlen signiert Client mit seinem geheimen Schlüssel.

Dann sendet Client nachfolgende Daten zum BBS:

versiegelte und signierte Zufallszahlen,
öffentlicher Schlüssel des Teilnehmers.

Im BBS erscheinen alle Daten. Erst nach dem Ende der Wahlzeit sendet Client die passenden Commitment-Schlüssel und die festgelegten Zufallszahlen zum BBS. Damit soll verhindert werden, daß niemand die Zufallszahlen vor Wahlzeitende kennt. Alle Zufallszahlen werden durch EXOR verknüpft, woraus eine EXOR-Summe hervorgeht. Aus dieser EXOR-Summe wird ein Repräsentant durch Anwenden der Entscheidungsfunktion ermittelt. Eine mögliche Manipulation der Ermittlung ohne den Einsatz der Commitment-Funktion würde z.B. darin bestehen, daß BBS mit einem Teilnehmer konspiriert. Die Zufallszahl des betreffenden Teilnehmers wird vom BBS als letzte Zahl, die empfangen wurde, gewertet. Dazu teilt BBS dem Teilnehmer die erforderliche Zufallszahl mit. Dadurch läßt sich die EXOR-Summe beliebig manipulieren. BBS kann aber auch den Signaturschlüssel eines Teilnehmers abkaufen und damit die erwünschte Zufallszahl mit Signatur selbst erzeugen.

Der Auswertungs-Server überprüft alle Commitments der Zufallszahlen auf Korrektheit. Für jede zu wählende repräsentative Position gehen anschließend die gültigen Zufallszahlen in eine Entscheidungsfunktion ein. Somit wird ein eindeutiger Kandidat ermittelt. Die Entscheidungsfunktion ist öffentlich bekannt. Ihr Bildbereich deckt die Menge der zu wählenden Kandidaten ab, d.h. ein Funktionswert entspricht genau einem Kandidaten. Die Methode der Abbildung der Zufallszahlen auf einen Kandidaten entspricht dabei einem zufälligen Selektionsprozeß, da die Input-Werte der Entscheidungsfunktion zufällig gewählt und erst nach Ablauf der Wahlzeit enthüllt werden.

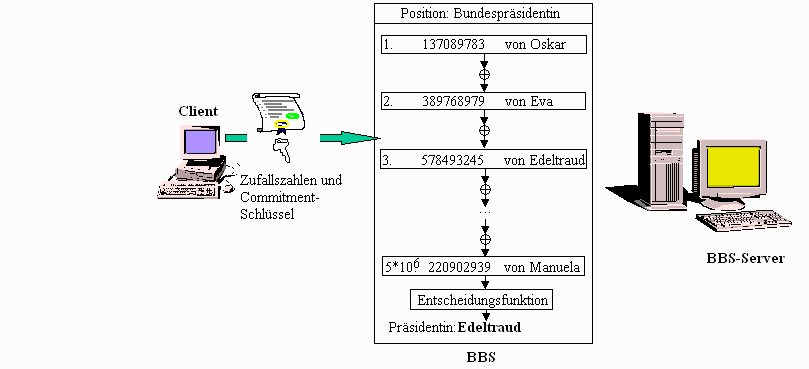
Abbildung 3.4: Repräsentantenwahl nach dem Zufallsprinzip.

Da BBS alle Zufallszahlen darstellt, kann jeder Teilnehmer prüfen, (1) ob seine Zufallszahl richtig verwendet wurde (individuelle Verifikation) und (2) ob der Auswertungsserver die Repräsentanten korrekt berechnet hat (universelle Verifikation).