3.7
Schemen des Alpha-Systems

Bevor das Alpha-System formalisiert wird, benötigen
wir Definitionen der eingesetzten Verschlüsselungs- und Signaturschemen.
3.7.1 Allgemeines
symmetrisches Verschlüsselungsschema
Ein symmetrisches Verschlüsselungsschema (ES,DS)
besteht aus drei Algorithmen, wobei
-
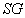 einen
Schlüsselgenerierungs-Algorithmus darstellt, der als Ausgabe einen
zufälligen Schlüssel ks liefert.
einen
Schlüsselgenerierungs-Algorithmus darstellt, der als Ausgabe einen
zufälligen Schlüssel ks liefert.
-
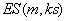 ein
Verschlüsselungs-Algorithmus ist, dessen Eingabe die Nachricht m
und den Schlüssel ks enthält. Als Ausgabewert wird der
Chiffretext
c geliefert.
ein
Verschlüsselungs-Algorithmus ist, dessen Eingabe die Nachricht m
und den Schlüssel ks enthält. Als Ausgabewert wird der
Chiffretext
c geliefert.
-
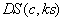 einen
Entschlüsselungs-Algorithmus repräsentiert, dessen Eingabewerte
aus dem Chiffretext c und dem Schlüssel ks bestehen.
Der Ausgabewert ergibt die entschlüsselte Nachricht m. Für
alle Nachrichten m und Schlüssel
ks
gilt
einen
Entschlüsselungs-Algorithmus repräsentiert, dessen Eingabewerte
aus dem Chiffretext c und dem Schlüssel ks bestehen.
Der Ausgabewert ergibt die entschlüsselte Nachricht m. Für
alle Nachrichten m und Schlüssel
ks
gilt 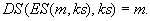
3.7.2 Allgemeines
asymmetrisches Verschlüsselungsschema
Ein Public-Key-Verschlüsselungsschema (E,D)
besteht aus drei Algorithmen, wobei
-
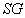 einen
Schlüsselgenerierungs-Algorithmus darstellt, dessen Ausgabe ein zufälliges
Schlüsselpaar
einen
Schlüsselgenerierungs-Algorithmus darstellt, dessen Ausgabe ein zufälliges
Schlüsselpaar 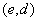 enthält.
Der öffentliche Schlüssel wird mit
enthält.
Der öffentliche Schlüssel wird mit 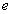 und
der geheime Schlüssel mit
und
der geheime Schlüssel mit 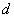 bezeichnet.
Die Schlüssellänge hängt vom momentanen Stand der Technik
ab.
bezeichnet.
Die Schlüssellänge hängt vom momentanen Stand der Technik
ab.
-
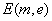 ein
Verschlüsselungs-Algorithmus ist, dessen Eingabewerte aus der Nachricht
ein
Verschlüsselungs-Algorithmus ist, dessen Eingabewerte aus der Nachricht 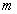 und
einem öffentlichen Schlüssel
und
einem öffentlichen Schlüssel 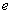 bestehen.
Die Ausgabe liefert den Chiffretext c.
bestehen.
Die Ausgabe liefert den Chiffretext c.
-
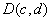 einen
Entschlüsselungs-Algorithmus bezeichnet. Die Eingabe setzt sich aus
dem Chiffretext
einen
Entschlüsselungs-Algorithmus bezeichnet. Die Eingabe setzt sich aus
dem Chiffretext 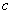 und
Schlüssel d zusammen. Der Ausgabewert ergibt somit die entschlüsselte
Nachricht m. Für alle Nachrichten m und Schlüsselpaare
und
Schlüssel d zusammen. Der Ausgabewert ergibt somit die entschlüsselte
Nachricht m. Für alle Nachrichten m und Schlüsselpaare 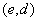 gilt
gilt 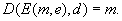
Falls nur der öffentliche Schlüssel 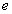 bekannt
ist, dann kann kein Krypto-Analytiker aus der verschlüsselten Nachricht
bekannt
ist, dann kann kein Krypto-Analytiker aus der verschlüsselten Nachricht 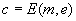 den
Klartext m in realistischer Zeit berechnen. Auch ist die Berechnung
des geheimen Schlüssels
den
Klartext m in realistischer Zeit berechnen. Auch ist die Berechnung
des geheimen Schlüssels 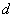 aus
dem öffentlichen Schlüssel e praktisch undurchführbar.
aus
dem öffentlichen Schlüssel e praktisch undurchführbar.
Ein einfaches hybrides Verschlüsselungsschema (EP,DP)
läßt sich durch die Kombination eines symmetrischen und asymmetrischen
Schlüsselschemas gewinnen. Zur Chiffrierung einer Nachricht m
-
wählt der Sender einen zufälligen symmetrischen
Schlüssel
p,
-
codiert den symmetrischen Schlüssel mit dem öffentlichen
Schlüssel
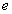 des
Empfängers, d.h.
des
Empfängers, d.h. 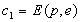 und
und
-
chiffriert die Nachricht m mit dem symmetrischen Schema
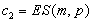
Daraus geht das Chiffretext-Paar 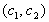 hervor.
hervor.
3.7.3 Allgemeines
digitales Signaturschema
Ein digitales Signaturschema (S,V) besteht aus
drei Algorithmen:
-
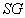 stellt
einen Schlüsselgenerierungs-Algorithmus dar, der als Ausgabewert ein
zufälliges Schlüsselpaar
stellt
einen Schlüsselgenerierungs-Algorithmus dar, der als Ausgabewert ein
zufälliges Schlüsselpaar 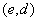 liefert,
wobei e den öffentlichen und
liefert,
wobei e den öffentlichen und 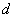 den
geheimen Schlüssel bezeichnet.
den
geheimen Schlüssel bezeichnet.
-
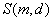 ist
ein Signatur-Algorithmus, dessen Eingabewerte aus der Nachricht m
und dem geheimen Schlüssel
ist
ein Signatur-Algorithmus, dessen Eingabewerte aus der Nachricht m
und dem geheimen Schlüssel 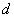 bestehen.
Die Ausgabe enthält die Signatur s zu m.
bestehen.
Die Ausgabe enthält die Signatur s zu m.
-
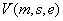 bezeichnet
einen Verifikations-Algorithmus, dessen Eingabewerte aus der Nachricht
m,
der Signatur s und dem öffentlichen Schlüssel
e bestehen.
bezeichnet
einen Verifikations-Algorithmus, dessen Eingabewerte aus der Nachricht
m,
der Signatur s und dem öffentlichen Schlüssel
e bestehen.
Falls eine Signaturprüfung mit dem öffentlichen
Schlüssel korrekt ist, dann liefert der Algorithmus den Ausgabewert
GÜLTIG,
sonst UNGÜLTIG.
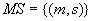 ist
eine endliche Menge von gültigen Paaren aus Nachricht und korrespondierender
Signatur, die mit dem öffentlichen Schlüssel
ist
eine endliche Menge von gültigen Paaren aus Nachricht und korrespondierender
Signatur, die mit dem öffentlichen Schlüssel 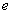 verifiziert
werden kann. Dann ist es praktisch unmöglich, weitere Signaturen ohne
verifiziert
werden kann. Dann ist es praktisch unmöglich, weitere Signaturen ohne 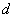 zu
erzeugen. Aus der Kenntnis von
zu
erzeugen. Aus der Kenntnis von 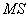 gewinnt
ein Angreifer keine Information über den geheimen Schlüssel d.
gewinnt
ein Angreifer keine Information über den geheimen Schlüssel d.
Um die Einmaligkeit und Zeitrichtigkeit der Signatur zu
gewährleisten, nehmen wir an, daß ein Zeitstempel vor dem Leisten
einer Signatur automatisch zur Nachricht m hinzugefügt wird.
Damit die Darstellung einfach bleibt, wird dieser Sachverhalt des weiteren
nicht explizit dargestellt. Bei der blinden Signatur wird kein Zeitstempel
hinzugefügt.
3.7.4 Hash-Funktion
Die Schemen wenden auch eine kryptographisch sichere Hash-Funktionen 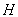 an,
deren Funktionswert die Länge t>128 Bit hat. Eine Funktion
an,
deren Funktionswert die Länge t>128 Bit hat. Eine Funktion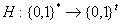 ist
eine Hash-Funktion, wenn diese die Menge beliebiger Binärzahlen in
die Menge der Binärzahlen mit fester Länge t abbildet.
Einfachheitshalber geben wir die Eingabeparameter der Hash-Funktion in
der Repräsentation ganzer Zahlen an. Wir nehmen an, daß tatsächlich
die binäre Darstellung benützt wird. Eine Hash-Funktion ist kryptographisch
sicher, wenn
ist
eine Hash-Funktion, wenn diese die Menge beliebiger Binärzahlen in
die Menge der Binärzahlen mit fester Länge t abbildet.
Einfachheitshalber geben wir die Eingabeparameter der Hash-Funktion in
der Repräsentation ganzer Zahlen an. Wir nehmen an, daß tatsächlich
die binäre Darstellung benützt wird. Eine Hash-Funktion ist kryptographisch
sicher, wenn
-
bei gegebenem Hash-Wert
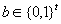 es
praktisch unmöglich ist, einen Wert
es
praktisch unmöglich ist, einen Wert 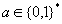 zu
finden, damit
zu
finden, damit 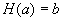 gilt
(Einwegfunktion),
gilt
(Einwegfunktion),
-
bei einem gegebenen Wert
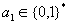 mit
vertretbarem Rechenaufwand kein
mit
vertretbarem Rechenaufwand kein 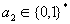 gefunden
werden kann
gefunden
werden kann 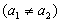 ,
so daß
,
so daß 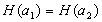 gilt
und
gilt
und
-
es praktisch undurchführbar ist, zwei beliebige Werte
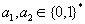 mit
mit 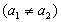 zu
finden, so daß
zu
finden, so daß 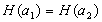 gilt
(Kollisionsfreiheit).
gilt
(Kollisionsfreiheit).
Die Eigenschaft der Kollisionsfreiheit verhindert den Geburtstagsangriff,
der darauf beruht, zwei zufällige und beliebige Nachrichten zu finden,
die den gleichen Hash-Funktionswert besitzen.
3.7.5 Notationen
Die administrativen Einheiten des Alpha-Systems sind die
lokalen Administrationen 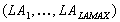 ,
die regionalen Administrationen
,
die regionalen Administrationen 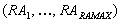 und
die nationalen Administrationen
und
die nationalen Administrationen 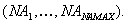 Bei
einer transnationalen E-Wahl existiert noch eine internationale Administration
IA.
Findet
eine landesweite Wahl statt, so steht die Administration des Bundeslandes
BLA
an
der Spitze des E-Wahlbaumes. Die BLA
erfüllt die gleichen Aufgaben
wie eine NA. Insgesamt können also
Bei
einer transnationalen E-Wahl existiert noch eine internationale Administration
IA.
Findet
eine landesweite Wahl statt, so steht die Administration des Bundeslandes
BLA
an
der Spitze des E-Wahlbaumes. Die BLA
erfüllt die gleichen Aufgaben
wie eine NA. Insgesamt können also 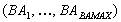 Bundesland-Administrationen
existieren.
Bundesland-Administrationen
existieren.
Jede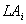 verfügt maximalistisch über ein
verfügt maximalistisch über ein
-
Zertifizierungssystem aus ZMAX Zertifizierungs-Servern
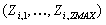 ,
,
-
Auswertungssystem aus AMAX Auswertungs-Servern
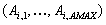 ,
,
-
Bulletin-Board-System aus BMAX Servern
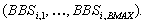
Normalerweise nehmen ZMAX, BMAX, AMAX den Wert 1 oder
2 an.
Jede regionale 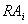 besitzt maximalistisch ein
besitzt maximalistisch ein
-
Inspektions-Server-System aus IMAX Inspektions-Servern
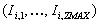 ,
,
-
Bulletin-Board-System aus BRMAX Servern
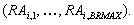
Bemerkung: Die Inspektions-Server werden von einer Gruppe
unabhängiger Personen kontrolliert.
Eine nationale Administration 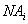 kontrolliert
NAMAX Server
kontrolliert
NAMAX Server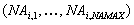 .
Auch die internationale Administration ist mit Servern ausgestattet.
.
Auch die internationale Administration ist mit Servern ausgestattet.
Um die Beschreibung zu vereinfachen, wird ohne Verlust
der Allgemeinheit auf einen exakten Index-Formalismus verzichtet und für
die Administrationen einfach LA, RA, NA, IA und für die Server
Z,
BBS, A, etc. geschrieben. Einer LA sind WMAX Wähler 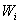
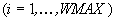 zugeordnet.
zugeordnet. 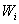 kontrolliert seinen Client
kontrolliert seinen Client 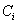 ,
der über einen geheimen Schlüssel
,
der über einen geheimen Schlüssel 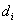 sowie
öffentlichen Schlüssel
sowie
öffentlichen Schlüssel 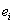 mit
einem Zertifikat
mit
einem Zertifikat 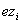 vom
Trust-Centerverfügt.
vom
Trust-Centerverfügt.
Den öffentlichen Schlüssel einer Instanz bezeichnen
wir mit 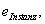 den
geheimen Schlüssel mit
den
geheimen Schlüssel mit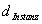 und
das zugehörige Zertifikat mit
und
das zugehörige Zertifikat mit 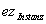 (z.B.
der Auswertungs-Server
(z.B.
der Auswertungs-Server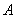 besitzt
ein asymmetrisches Schlüsselpaar
besitzt
ein asymmetrisches Schlüsselpaar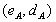 mit
einem Zertifikat
mit
einem Zertifikat 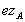 vom
Trust-Center). Des weiteren wird eine eindeutig zerlegbare Verkettung zweier
Werte
vom
Trust-Center). Des weiteren wird eine eindeutig zerlegbare Verkettung zweier
Werte 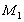 und
und 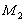 durch
das Symbol "
durch
das Symbol "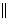 "
dargestellt, d.h.
"
dargestellt, d.h.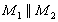 .
.
3.7.6 Vorbereitung
Im System Alpha-1 bis Alpha-4 werden die nachfolgenden
Schritte in der Vorbereitungsphase vorgenommen. Der Auswertungs-Server
jeder lokalen Administration LA erzeugt zunächst eine Teilnehmerliste
(Id, Name, Teilnahme, öffentlicher Teilnehmerschlüssel).
Die Daten zur Erstellung der Teilnehmerliste gewinnt A aus den Einträgen
des X.500-Verzeichnisses (CCITT X.500, 1994). Das Attribut Teilnahme
nimmt einen Wert der Menge {JA, NEIN} an und verhindert die
Mehrfachzählung. Alle Einträge des Attributes Teilnahme werden
auf NEIN initialisiert.
Die Datenstruktur spez besteht mindestens aus den
nachstehenden Informationen:
-
Entscheidungsart,
-
Beginn der Entscheidung,
-
Ende der Entscheidung,
-
Formatspezifikation für Entscheidung/Initiative (Die
Formatspezifikation definiert die Gestalt gültiger Entscheidungen
(Anzahl der Optionen, Gültigkeitsbereiche, Identifizierungsnummer
der Entscheidung etc.).).
BBS unterzeichnet die Spezifikation 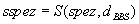 mit
seinem geheimen Schlüssel
mit
seinem geheimen Schlüssel 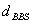 und
veröffentlicht
und
veröffentlicht 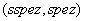 im
X.500.
im
X.500.
Der jeweilige Client lädt alle nötigen Daten
und Schlüssel aus dem X.500-Verzeichnis. Für alle Protokolle
wird angenommen, daß der Anwender sich vor der Stimmabgabe bzw. vor
der Unterzeichnung einer Initiative gegenüber Client mit einem Paßwort
authentifizieren muß.
3.7.7 Alpha-1-Protokoll
Jeder Client 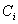 signiert
die Spezifikation der Initiative
signiert
die Spezifikation der Initiative 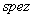 mit
seinem geheimen Schlüssel, d.h.
mit
seinem geheimen Schlüssel, d.h. 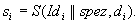
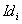 ist
die Identität von
ist
die Identität von 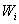 .
.
-
Der Client sendet
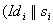
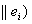 zum
BBS.
zum
BBS.
-
Der Auswertungs-Server überprüft, ob
-
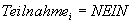 und
und
-
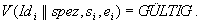
-
Wenn beide Bedingungen erfüllt sind, setzt A
das entsprechende Attribut Teilnahme auf den Wert JA und
inkrementiert seinen Zählerstand.
Alle Signaturen werden in der Auswertungsliste im BBS
dargestellt,
die aus den Daten (Teilnehmeridentität, öffentlicher
Teilnehmerschlüssel, Zertifikat, Client-Signatur) bestehen.
3.7.8 Alpha-2-Protokoll
-
Jeder Client generiert ein Zufallsschlüsselpaar
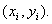 Mit
dem geheimen Schlüssel
Mit
dem geheimen Schlüssel 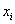 signiert
der Client die Spezifikation der E-Initiative, d.h.
signiert
der Client die Spezifikation der E-Initiative, d.h. 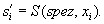 Diese
Pseudonym-Signatur unterzeichnet
Diese
Pseudonym-Signatur unterzeichnet 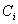 mit
seinem Geheimschlüssel
mit
seinem Geheimschlüssel 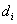 und
erhält
und
erhält 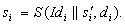
-
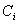 verschlüsselt
beide Signaturen mit Hilfe eines zufälligen symmetrischen Schlüssels
verschlüsselt
beide Signaturen mit Hilfe eines zufälligen symmetrischen Schlüssels 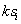 (hybride
Verschlüsselung). Letzterer wird wiederum mit dem öffentlichen
Schlüssel von A codiert:
(hybride
Verschlüsselung). Letzterer wird wiederum mit dem öffentlichen
Schlüssel von A codiert: 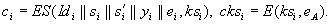
-
Jeder Client sendet seine verschlüsselten Signaturen
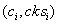
zum Auswertungs-Server.
Bemerkung: Die hybride Verschlüsselung wird eingesetzt,
da der längere Plaintext (2 Signaturen, 2 Schlüssel, etc.) im
Vergleich zur asymmetrischen Codierung schneller verschlüsselt werden
kann.
A publiziert alle Pseudonym-Signaturen 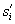 und
die korrespondierenden öffentlichen Schlüssel
und
die korrespondierenden öffentlichen Schlüssel 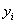 im
BBS,
damit
die Teilnehmer die Auswertung verifizieren können.
im
BBS,
damit
die Teilnehmer die Auswertung verifizieren können.
3.7.9 Alpha-3-Protokoll
Im Alpha-3-Protokoll gewinnt das Protokoll zur Erzeugung
des Kollektivschlüssels zentrale Bedeutung.
3.7.9.1 Kollektivschlüssel-Erzeugungsprotokoll
Dieses Secret-Sharing-Schema teilt einen geheimen Kollektivschlüssel 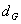 in
J
Teile auf, wobei jedes Mitglied des kollektiven Dechiffrierungskreises
einen Teil erhält. Erst wenn alle J Teile in den Decodierungsprozeß
eingehen, kann eine mit dem öffentlichen Kollektivschlüssel codierte
Nachricht entschlüsselt werden.
in
J
Teile auf, wobei jedes Mitglied des kollektiven Dechiffrierungskreises
einen Teil erhält. Erst wenn alle J Teile in den Decodierungsprozeß
eingehen, kann eine mit dem öffentlichen Kollektivschlüssel codierte
Nachricht entschlüsselt werden.
RA und die ihr zugeordneten Auswertungs-Server
partizipieren beim robusten verifizierbaren Secret-Sharing-Protokoll. Jeder
Protokollteilnehmer erzeugt einen geheimen Teilschlüssel 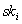 und
einen öffentlichen Teilschlüssel
und
einen öffentlichen Teilschlüssel 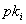 .
Alle öffentlichen Teilschlüssel werden im BBS der RA
publiziert. Zudem beweist der Teilnehmer, daß er
.
Alle öffentlichen Teilschlüssel werden im BBS der RA
publiziert. Zudem beweist der Teilnehmer, daß er 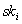 kennt,
ohne den Wert
kennt,
ohne den Wert 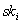 zu
enthüllen, indem dieser
zu
enthüllen, indem dieser 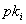 signiert, d.h.
signiert, d.h. 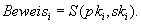 Das
ist ein Beweis, da jeder Teilnehmer ohne Kenntnis des geheimen Schlüssels
durch die öffentliche Verifikationsfunktion V überprüfen
kann, ob
Das
ist ein Beweis, da jeder Teilnehmer ohne Kenntnis des geheimen Schlüssels
durch die öffentliche Verifikationsfunktion V überprüfen
kann, ob 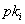 und
und 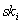 korrespondieren.
Mithin können die Beteiligten prüfen, ob
korrespondieren.
Mithin können die Beteiligten prüfen, ob 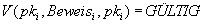 ist.
ist.
Sobald mindestens ein Auswertungs-Server fehlerhaft funktioniert,
terminiert das Protokoll. Der öffentliche Kollektivschlüssel
läßt sich durch Anwendung einer Aggregationsfunktion AG gewinnen,
d.h. 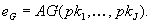 Die
genaue Gestalt dieser Funktion wird später dargestellt. Der Algorithmus
stellt sicher, daß kein Auswertungs-Server den geheimen Kollektivschlüssel
Die
genaue Gestalt dieser Funktion wird später dargestellt. Der Algorithmus
stellt sicher, daß kein Auswertungs-Server den geheimen Kollektivschlüssel 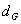 kennt. Hält mindestens ein Teilnehmer seinen Teilschlüssel
kennt. Hält mindestens ein Teilnehmer seinen Teilschlüssel 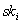 geheim,
so ist niemand imstande, Wahlscheine vorzeitig zu entschlüsseln. Der
geheime Kollektivschlüssel
geheim,
so ist niemand imstande, Wahlscheine vorzeitig zu entschlüsseln. Der
geheime Kollektivschlüssel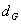 besteht
aus der Summe
besteht
aus der Summe 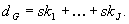 Bemerkung: „+“ bezeichnet hier eine Addition ganzer Zahlen.
Bemerkung: „+“ bezeichnet hier eine Addition ganzer Zahlen.
Es wird angenommen, daß die RA den
Teilschlüssels 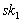 besitzt. Die weiteren geheimen Teilschlüssel kontrollieren ihre untergeordneten
Auswertungs-Server. Findet nur eine lokale Wahl statt (J=2), dann
wird der geheime Kollektivschlüssel zwischen RA und dem entsprechenden
Auswertungs-Server der LA geteilt.
besitzt. Die weiteren geheimen Teilschlüssel kontrollieren ihre untergeordneten
Auswertungs-Server. Findet nur eine lokale Wahl statt (J=2), dann
wird der geheime Kollektivschlüssel zwischen RA und dem entsprechenden
Auswertungs-Server der LA geteilt.
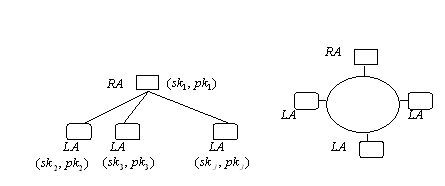
Abbildung 3.15: Verteilung des geheimen Kollektivschlüssels
auf den Dechiffrierungskreis (Alpha-3-System).
3.7.9.2 Wahlprotokoll
-
Der Wahlschein ist
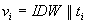 .
IDW
ist
eine Identifizierungsnummer, die eine bestimmte Entscheidung (bzw. Wahl)
eindeutig identifiziert und in der Datenstruktur spez enthalten
ist.
.
IDW
ist
eine Identifizierungsnummer, die eine bestimmte Entscheidung (bzw. Wahl)
eindeutig identifiziert und in der Datenstruktur spez enthalten
ist. 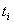 ist
das Votum des Teilnehmers. Der Client wählt eine Zufallszahl
ist
das Votum des Teilnehmers. Der Client wählt eine Zufallszahl 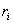 und
chiffriert seine Wahlstrategie
und
chiffriert seine Wahlstrategie 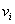 durch
die Anwendung des Kollektivschlüssels
durch
die Anwendung des Kollektivschlüssels 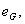 d.h.
d.h. 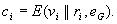
-
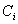 signiert
den verschlüsselten Wert
signiert
den verschlüsselten Wert 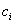 mit
seinem geheimen Schlüssel
mit
seinem geheimen Schlüssel 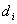 ,
d.h.
,
d.h. 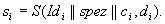
-
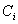 sendet
sendet 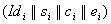 zum BBS.
zum BBS.
Bemerkung: Public-Key-Kryptosysteme sind durch Chosen-Plaintext/Chiphertext-Angriffe
gefährdet. Dieser Angriff ist besonders wirksam, wenn die Anzahl der
möglichen verschlüsselten Voten gering ist. Daher wird eine Zufallszahl
zum Wahlschein angefügt.
3.7.9.3 Auswertungsprotokoll
-
Nach Ende der Wahlzeit sendet jede LA an RA
ihren geheimen Teilschlüssel.
-
RA publiziert alle geheimen Teilschlüssel
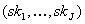 sowie
sowie 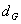 in
ihrem BBS.
in
ihrem BBS.
-
Die Auswertungs-Server laden
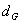 vom
RA-BBS
und
starten mit ihrer Auswertung.
vom
RA-BBS
und
starten mit ihrer Auswertung.
-
Jeder Auswertungs-Server überprüft alle Signaturen
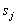
und dechiffriert alle codierten Wahlscheine. Die entschlüsselten
Wahlscheine überträgt A zusammen mit dem Resultat zu ihrem
BBS.
3.7.10 Alpha-4-Protokoll
Das Alpha-4-Protokoll realisiert die Auswahl von k
Repräsentanten aus einer Menge von n Kandidaten 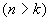 nach
dem Zufallsprinzip. Jedem Kandidaten wird eine eindeutige Zahl der Menge
nach
dem Zufallsprinzip. Jedem Kandidaten wird eine eindeutige Zahl der Menge 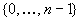 zugeordnet.
zugeordnet.
3.7.10.1 Zufallswahl-Protokoll
-
Client
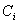 generiert
generiert 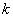 Pseudo-Zufallszahlen
Pseudo-Zufallszahlen 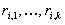 und
korrespondierende Commitment-Schlüssel
und
korrespondierende Commitment-Schlüssel 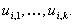 Jede
gültige Zufallszahl ist ein Element der Menge
Jede
gültige Zufallszahl ist ein Element der Menge 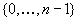 .
. 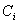 verschlüsselt
jede Zufallszahl
verschlüsselt
jede Zufallszahl 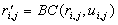 durch
die Commitment-Funktion, signiert
durch
die Commitment-Funktion, signiert 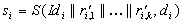 und
sendet die Werte
und
sendet die Werte 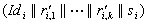 zum
BBS.
BBS
publiziert
jedes empfangene Paket in einer öffentlichen Liste.
zum
BBS.
BBS
publiziert
jedes empfangene Paket in einer öffentlichen Liste.
-
Nach dem Ablauf der Wahlzeit transferiert jeder Teilnehmer
seine Commitment-Schlüssel
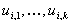 und
die Zufallszahlen
und
die Zufallszahlen 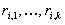 mit der Angabe der Listenposition l zum BBS. Letztere wird
benötigt, um die Position der Protokolldaten von
mit der Angabe der Listenposition l zum BBS. Letztere wird
benötigt, um die Position der Protokolldaten von 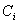 im
BBS zu adressieren.
im
BBS zu adressieren.
-
Der Auswertungs-Server überprüft zunächst
alle Commitments. Dem Auswertungsserver muß nicht vertraut werden,
da alle Protokollwerte und die Funktion zur Ermittlung der Kandidaten öffentlich
bekannt sind. Daher ist die Verifikation der Korrektheit der Ermittlung
durch die Öffentlichkeit gegeben. Jeder Teilnehmer kann die ordnungsgemäße
Auswertung nachprüfen. Die Entscheidungsfunktion besteht im ersten
Schritt darin, daß jeweils die (bitweise) EXOR-Verknüpfung aller
mit einer repräsentativen Position korrespondierenden Zufallszahlen
gebildet wird, woraus wieder ein Zufalls-Output hervorgeht. TMAX bezeichnet
im folgenden die Anzahl der Teilnehmer, die gültige Zufallszahlen
übermittelten.
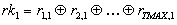
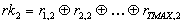
.....................................
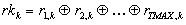
-
Der Auswertungs-Server bestimmt die k Repräsentanten:
Wenn die Ermittlungsfunktion auf Repräsentanten abbildet,
die schon vorher einmal ausgewählt wurden, dann ist eine Kandidatenkollision
aufgetreten und folglich muß der Auswertungs-Server eine Kollisions-Auflösungsmethode
exekutieren: A entfernt alle 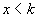 gewählten
Repräsentanten aus der Menge
gewählten
Repräsentanten aus der Menge 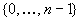 .
Jedem verbleibenden Kandidaten wird wiederum eine eindeutige Zahl der Restmenge
.
Jedem verbleibenden Kandidaten wird wiederum eine eindeutige Zahl der Restmenge 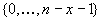 zugeordnet.
Daraus werden die restlichen
zugeordnet.
Daraus werden die restlichen 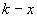 Kandidaten
durch einen neuen Durchgang des Protokolls selektiert. Der Ansatz kann
mehrere Durchgänge erfordern, wenn Kollisionen wieder eintreten.
Kandidaten
durch einen neuen Durchgang des Protokolls selektiert. Der Ansatz kann
mehrere Durchgänge erfordern, wenn Kollisionen wieder eintreten.
Im BBS steht nach dem Protokollende eine Liste
der auserwählten Repräsentanten:
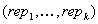 .
Für die selektierten Personen können zwei Alternativen
eintreten
.
Für die selektierten Personen können zwei Alternativen
eintreten 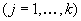 :
:
-
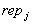 nimmt
die Wahl an, indem diese mit seiner Signatur zustimmt, oder
nimmt
die Wahl an, indem diese mit seiner Signatur zustimmt, oder
-
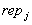 lehnt
die Auswahl mit signierter Begründung ab.
lehnt
die Auswahl mit signierter Begründung ab.
Existiert eine Restmenge 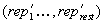 von
Personen, die ihre Position nicht antreten wollen, so erfolgt ein neuer
Durchgang, um zufällig gewählte Ersatzkandidaten zu ermitteln:
Für die neuen Kandidaten besteht wieder Wahlfreiheit, zwischen den
beiden oben beschriebenen Alternativen zu wählen.
von
Personen, die ihre Position nicht antreten wollen, so erfolgt ein neuer
Durchgang, um zufällig gewählte Ersatzkandidaten zu ermitteln:
Für die neuen Kandidaten besteht wieder Wahlfreiheit, zwischen den
beiden oben beschriebenen Alternativen zu wählen.





![]() ist
eine endliche Menge von gültigen Paaren aus Nachricht und korrespondierender
Signatur, die mit dem öffentlichen Schlüssel
ist
eine endliche Menge von gültigen Paaren aus Nachricht und korrespondierender
Signatur, die mit dem öffentlichen Schlüssel ![]() verifiziert
werden kann. Dann ist es praktisch unmöglich, weitere Signaturen ohne
verifiziert
werden kann. Dann ist es praktisch unmöglich, weitere Signaturen ohne ![]() zu
erzeugen. Aus der Kenntnis von
zu
erzeugen. Aus der Kenntnis von ![]() gewinnt
ein Angreifer keine Information über den geheimen Schlüssel d.
gewinnt
ein Angreifer keine Information über den geheimen Schlüssel d.
![]() an,
deren Funktionswert die Länge t>128 Bit hat. Eine Funktion
an,
deren Funktionswert die Länge t>128 Bit hat. Eine Funktion![]() ist
eine Hash-Funktion, wenn diese die Menge beliebiger Binärzahlen in
die Menge der Binärzahlen mit fester Länge t abbildet.
Einfachheitshalber geben wir die Eingabeparameter der Hash-Funktion in
der Repräsentation ganzer Zahlen an. Wir nehmen an, daß tatsächlich
die binäre Darstellung benützt wird. Eine Hash-Funktion ist kryptographisch
sicher, wenn
ist
eine Hash-Funktion, wenn diese die Menge beliebiger Binärzahlen in
die Menge der Binärzahlen mit fester Länge t abbildet.
Einfachheitshalber geben wir die Eingabeparameter der Hash-Funktion in
der Repräsentation ganzer Zahlen an. Wir nehmen an, daß tatsächlich
die binäre Darstellung benützt wird. Eine Hash-Funktion ist kryptographisch
sicher, wenn
![]() ,
die regionalen Administrationen
,
die regionalen Administrationen ![]() und
die nationalen Administrationen
und
die nationalen Administrationen ![]() Bei
einer transnationalen E-Wahl existiert noch eine internationale Administration
IA.
Findet
eine landesweite Wahl statt, so steht die Administration des Bundeslandes
BLA
an
der Spitze des E-Wahlbaumes. Die BLA
erfüllt die gleichen Aufgaben
wie eine NA. Insgesamt können also
Bei
einer transnationalen E-Wahl existiert noch eine internationale Administration
IA.
Findet
eine landesweite Wahl statt, so steht die Administration des Bundeslandes
BLA
an
der Spitze des E-Wahlbaumes. Die BLA
erfüllt die gleichen Aufgaben
wie eine NA. Insgesamt können also ![]() Bundesland-Administrationen
existieren.
Bundesland-Administrationen
existieren.
![]() verfügt maximalistisch über ein
verfügt maximalistisch über ein
![]() besitzt maximalistisch ein
besitzt maximalistisch ein
![]() kontrolliert
NAMAX Server
kontrolliert
NAMAX Server![]() .
Auch die internationale Administration ist mit Servern ausgestattet.
.
Auch die internationale Administration ist mit Servern ausgestattet.
![]()
![]() zugeordnet.
zugeordnet. ![]() kontrolliert seinen Client
kontrolliert seinen Client ![]() ,
der über einen geheimen Schlüssel
,
der über einen geheimen Schlüssel ![]() sowie
öffentlichen Schlüssel
sowie
öffentlichen Schlüssel ![]() mit
einem Zertifikat
mit
einem Zertifikat ![]() vom
Trust-Centerverfügt.
vom
Trust-Centerverfügt.
![]() den
geheimen Schlüssel mit
den
geheimen Schlüssel mit![]() und
das zugehörige Zertifikat mit
und
das zugehörige Zertifikat mit ![]() (z.B.
der Auswertungs-Server
(z.B.
der Auswertungs-Server![]() besitzt
ein asymmetrisches Schlüsselpaar
besitzt
ein asymmetrisches Schlüsselpaar![]() mit
einem Zertifikat
mit
einem Zertifikat ![]() vom
Trust-Center). Des weiteren wird eine eindeutig zerlegbare Verkettung zweier
Werte
vom
Trust-Center). Des weiteren wird eine eindeutig zerlegbare Verkettung zweier
Werte ![]() und
und ![]() durch
das Symbol "
durch
das Symbol "![]() "
dargestellt, d.h.
"
dargestellt, d.h.![]() .
.
![]() signiert
die Spezifikation der Initiative
signiert
die Spezifikation der Initiative ![]() mit
seinem geheimen Schlüssel, d.h.
mit
seinem geheimen Schlüssel, d.h. ![]()
![]() ist
die Identität von
ist
die Identität von ![]() .
.
![]() und
die korrespondierenden öffentlichen Schlüssel
und
die korrespondierenden öffentlichen Schlüssel ![]() im
BBS,
damit
die Teilnehmer die Auswertung verifizieren können.
im
BBS,
damit
die Teilnehmer die Auswertung verifizieren können.
![]() in
J
Teile auf, wobei jedes Mitglied des kollektiven Dechiffrierungskreises
einen Teil erhält. Erst wenn alle J Teile in den Decodierungsprozeß
eingehen, kann eine mit dem öffentlichen Kollektivschlüssel codierte
Nachricht entschlüsselt werden.
in
J
Teile auf, wobei jedes Mitglied des kollektiven Dechiffrierungskreises
einen Teil erhält. Erst wenn alle J Teile in den Decodierungsprozeß
eingehen, kann eine mit dem öffentlichen Kollektivschlüssel codierte
Nachricht entschlüsselt werden.
![]() und
einen öffentlichen Teilschlüssel
und
einen öffentlichen Teilschlüssel ![]() .
Alle öffentlichen Teilschlüssel werden im BBS der RA
publiziert. Zudem beweist der Teilnehmer, daß er
.
Alle öffentlichen Teilschlüssel werden im BBS der RA
publiziert. Zudem beweist der Teilnehmer, daß er ![]() kennt,
ohne den Wert
kennt,
ohne den Wert ![]() zu
enthüllen, indem dieser
zu
enthüllen, indem dieser ![]() signiert, d.h.
signiert, d.h. ![]() Das
ist ein Beweis, da jeder Teilnehmer ohne Kenntnis des geheimen Schlüssels
durch die öffentliche Verifikationsfunktion V überprüfen
kann, ob
Das
ist ein Beweis, da jeder Teilnehmer ohne Kenntnis des geheimen Schlüssels
durch die öffentliche Verifikationsfunktion V überprüfen
kann, ob ![]() und
und ![]() korrespondieren.
Mithin können die Beteiligten prüfen, ob
korrespondieren.
Mithin können die Beteiligten prüfen, ob ![]() ist.
ist.
![]() Die
genaue Gestalt dieser Funktion wird später dargestellt. Der Algorithmus
stellt sicher, daß kein Auswertungs-Server den geheimen Kollektivschlüssel
Die
genaue Gestalt dieser Funktion wird später dargestellt. Der Algorithmus
stellt sicher, daß kein Auswertungs-Server den geheimen Kollektivschlüssel ![]() kennt. Hält mindestens ein Teilnehmer seinen Teilschlüssel
kennt. Hält mindestens ein Teilnehmer seinen Teilschlüssel ![]() geheim,
so ist niemand imstande, Wahlscheine vorzeitig zu entschlüsseln. Der
geheime Kollektivschlüssel
geheim,
so ist niemand imstande, Wahlscheine vorzeitig zu entschlüsseln. Der
geheime Kollektivschlüssel![]() besteht
aus der Summe
besteht
aus der Summe ![]() Bemerkung: „+“ bezeichnet hier eine Addition ganzer Zahlen.
Bemerkung: „+“ bezeichnet hier eine Addition ganzer Zahlen.
![]() besitzt. Die weiteren geheimen Teilschlüssel kontrollieren ihre untergeordneten
Auswertungs-Server. Findet nur eine lokale Wahl statt (J=2), dann
wird der geheime Kollektivschlüssel zwischen RA und dem entsprechenden
Auswertungs-Server der LA geteilt.
besitzt. Die weiteren geheimen Teilschlüssel kontrollieren ihre untergeordneten
Auswertungs-Server. Findet nur eine lokale Wahl statt (J=2), dann
wird der geheime Kollektivschlüssel zwischen RA und dem entsprechenden
Auswertungs-Server der LA geteilt.

![]() nach
dem Zufallsprinzip. Jedem Kandidaten wird eine eindeutige Zahl der Menge
nach
dem Zufallsprinzip. Jedem Kandidaten wird eine eindeutige Zahl der Menge ![]() zugeordnet.
zugeordnet.