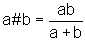Diesmal hat es etwas länger gedauert, weil ich zu Semesterbeginn ziemlich im Stress war. Bitte um Entschuldigung!
Heute möchte ich euch eine kleine Spielerei von mir vorstellen.
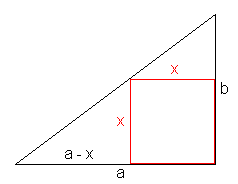 Welche Seitenlänge hat das Quadrat, das man in ein rechtwinkeliges Dreieck mit den Katheten a und b
einschreiben kann?
Welche Seitenlänge hat das Quadrat, das man in ein rechtwinkeliges Dreieck mit den Katheten a und b
einschreiben kann?
In der Zeichnung erkennt man die Proportion a : b = (a - x) : x. Daraus erhält man
x = ab/(a + b) bzw. 1/x = 1/a + 1/b.
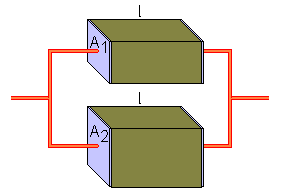 Wenn zwei elektrische Widerstände R1 und R2 parallel geschaltet werden, ergibt sich der Gesamtwiderstand R
nach der Formel
Wenn zwei elektrische Widerstände R1 und R2 parallel geschaltet werden, ergibt sich der Gesamtwiderstand R
nach der Formel
1/R = 1/R1 + 1/R2
(Ein Klick auf das Bild führt zu einem Wikipedia-Artikel mit genaueren Erklärungen.)
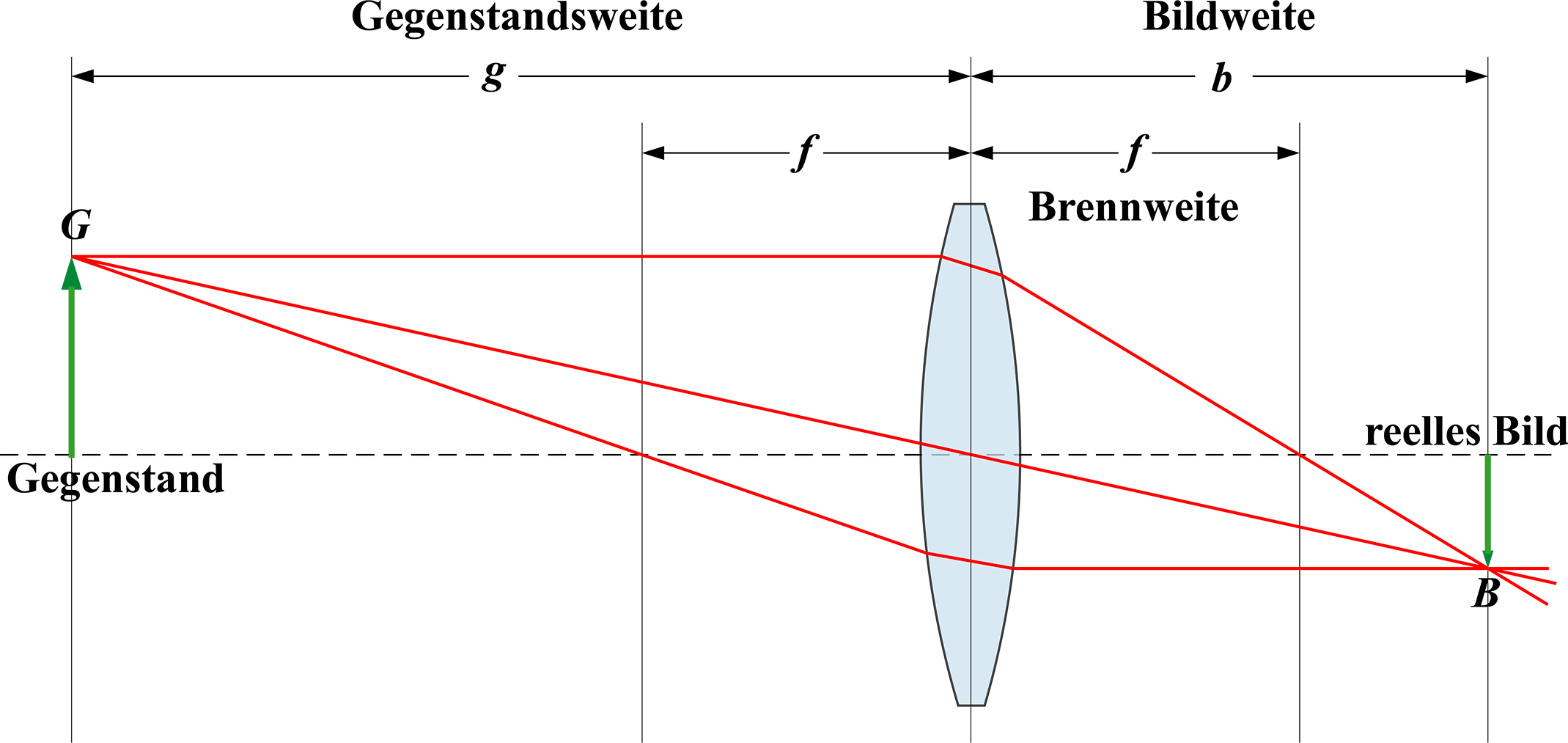 Ein Gegenstand wird von einer Sammellinse abgebildet. Man kennt die Brennweite f (den Abstand des Brennpunkts von
der Linse) und die Gegenstandweite g (den Abstand des Gegenstands von der Linse). Die Bildweite b kann man
dann nach der sogenannten Linsengleichung berechnen:
Ein Gegenstand wird von einer Sammellinse abgebildet. Man kennt die Brennweite f (den Abstand des Brennpunkts von
der Linse) und die Gegenstandweite g (den Abstand des Gegenstands von der Linse). Die Bildweite b kann man
dann nach der sogenannten Linsengleichung berechnen:
1/f = 1/g + 1/b
(Auch hier bitte das Bild anklicken!)
 Die Erde braucht für einen Umlauf um die Sonne 365 Tage, der Mars 687 Tage. Nach welcher Zeit haben Erde und Mars
wieder die gleiche Stellung zueinander?
Die Erde braucht für einen Umlauf um die Sonne 365 Tage, der Mars 687 Tage. Nach welcher Zeit haben Erde und Mars
wieder die gleiche Stellung zueinander?
Die Erde legt pro Tag 1/365 eines vollen Umlaufs zurück, der Mars 1/687. Die Erde gewinnt pro Tag also
1/365 - 1/687 ~ 1/779 eines Umlaufs Vorsprung. Nach 779 Tagen, also ca. nach 2 Jahren und 2 Monaten, hat sie den Mars
einmal überrundet.
Allgemein ergibt sich für die sogenannte synodische Umlaufzeit eines Planeten die Formel
1/T = 1/T1 - 1/T2
(Das Bild - auch hier anklickbar - entspricht nicht den angegebenen Zahlen.)
 Seifenblasen haben bekanntlich (wegen der Oberflächenspannung) immer Kugelform. Wenn zwei verschieden große
Seifenblasen mit den Radien r1 und r2 zusammenhängen, nimmt die Trennwand auch die Form
eines Kugelabschnitts (mit Radius r3) an, der sich etwas in die größere Blase hineinwölbt. Dort, wo die Seifenhäute zusmmenstoßen,
bilden sie miteinander Winkel von 120° (weil die Spannungskräfte im Gleichgewicht sein müssen). Man kann zeigen, dass
für die Radien gilt
Seifenblasen haben bekanntlich (wegen der Oberflächenspannung) immer Kugelform. Wenn zwei verschieden große
Seifenblasen mit den Radien r1 und r2 zusammenhängen, nimmt die Trennwand auch die Form
eines Kugelabschnitts (mit Radius r3) an, der sich etwas in die größere Blase hineinwölbt. Dort, wo die Seifenhäute zusmmenstoßen,
bilden sie miteinander Winkel von 120° (weil die Spannungskräfte im Gleichgewicht sein müssen). Man kann zeigen, dass
für die Radien gilt
1/r3 = 1/r1 - 1/r2
Dass diese Form wirklich optimal ist - das sogenannte double bubble theorem -, wurde übrigens erst 2000 bewiesen.
(Die Computergraphik stammt von der Homepage von Prof. John M. Sullivan.)
Und schließlich erinnert auch die Definition des harmonischen Mittels (siehe
Mathe-Newsletter 14)
an diese Formeln:
1/H(a,b) = 1/2·(1/a + 1/b)
Bei allen diesen Formeln werden Kehrwerte addiert. Das hat mich auf die Idee gebracht, diese Rechenoperation
zu untersuchen. Ich nenne sie "Kehrwertaddition" und bezeichne sie mit # (weil ich dieses Zeichen sonst nicht brauche).
Wir definieren also
Beispiel: 3 # 6 = 2, weil 1/3 + 1/6 = 1/2.
Man kann leicht einsehen, dass # kommutativ und assoziativ ist. (Es ist 1/a + 1/b = 1/b + 1/a
und 1/a + (1/b + 1/c) = (1/a + 1/b) + 1/c, also sind auch die Kehrwerte gleich).
Die Kehrwertaddition mit 0 ist nach der ersten Definition sinnlos, nach der zweiten Definition erhält man
a # b = 0 sein, wenn entweder a = 0 oder
b = 0 ist (ähnlich wie bei der Multiplikation).
Während bei der normalen Adddtion die Summe größer ist als die einzelnen Summanden, gilt für die Kehrwertaddition
das Gegenteil: a # b ist kleiner als a und b (zumindest solange a und b positiv sind).
Wenn wir die
Konstruktion aus dem ersten Beispiel ein bisschen abändern (den Winkel von 90° auf 120° vergrößern), erhalten wir eine
schöne graphische Darstellung: Wir zeichnen drei Skalen jeweils im Winkel von 60°. Wenn wir a auf der ersten Skala
und b auf der letzten Skala durch eine gerade Linie verbinden, können wir im Schnittpunkt mit der mittleren Skala
das Ergebnis a # b ablesen:
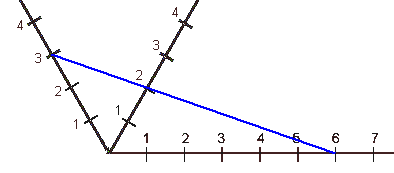
Die obigen Formeln können wir jetzt kürzer so schreiben:
- Quadrat im rechtwinkeligen Dreieck: x = a # b
- Widerstand bei Parallelschaltung: R = R1 # R2
- Linsengleichung: f = g # b
- Synodische Umlaufzeit: T = T1 # (-T2)
- Seifenblasen: r3 = r1 # (-r2)
- Harmonisches Mittel: H(a,b) = 2(a # b)
Kurze Einführung in die Gruppentheorie
Rechenoperationen wie Addition und Multiplikation bezeichnet man auch als Verknüpfungen: zwei Zahlen werden miteinander
verknüpft, und das Ergebnis ist eine neue Zahl - die Summe bzw. das Produkt. Sie haben einige Gemeinsamkeiten: Es gilt z.B. das Kommutativgesetz und
das Assoziativgesetz. Es gibt ein Element, das nichts ändert: die 0 bei der Addition, die 1 bei der Multiplikation.
Und jede Rechnung kann wieder rückgängig gemacht werden: +a durch +(-a), ·a durch ·1/a.
Diese Eigenschaften treten auch bei anderen Verknüpfungen auf. In der Algebra bezeichnet man so etwas als Gruppen
und untersucht ihre Eigenschaften. So kann man Gemeinsamkeiten zwischen Strukturen feststellen, die auf den ersten Blick ganz
verschieden aussehen.
Wir bezeichnen jetzt mit M irgendeine Menge und mit ◦ eine beliebige Verknüpfung. (M,◦) ist eine Gruppe, wenn
folgende Bedingungen erfüllt sind:
- M ist abgeschlossen gegenüber ◦, das heißt, wenn man zwei Elemente von M miteinander
verknüpft, erhält man wieder ein Element von M.
- Die Verknüpfung ist assoziativ, das heißt, a◦(b◦c) = (a◦b)◦c
für alle a, b, c aus M.
- Es gibt in M ein neutrales Element n, so dass a◦n = n◦a = a für alle a aus M.
- Zu jedem Element a gibt es ein inverses Element a', so dass a◦a' = a'◦a = n.
- Wenn die Verknüpfung außerdem noch kommutativ ist, das heißt a◦b = b◦a für alle a, b aus M,
spricht man von einer kommutativen oder Abelschen Gruppe.
Nach dieser Definition sind z.B. (Z,+), (Q,+) und (R,+) kommutative Gruppen, ebenso wie (Q\{0},·) und (R\{0},·).
Bei der Multiplikation muss man 0 auschließen, weil es dazu kein inverses Element gibt (1/0 ist nicht definiert).
Weitere Beispiele für Gruppen sind die Restklassenaddition, die Restklassenmultiplikation modulo einer Primzahl
(siehe Mathe-Newsletter 2),
aber auch die sogenannten Symmetriegruppen, das heißt die Drehungen und Spiegelungen, die eine symmetrische Figur (z.B. ein Quadrat oder einen Würfel) auf sich
selbst abbilden.
Wir wollen jetzt untersuchen, ob wir mit der Kehrwertaddition eine Gruppe erhalten. Dafür nehmen wir zu den reellen Zahlen
noch das Element ∞ dazu. Die Vereinigungsmenge von R und {∞} heißt erweiterte reelle Zahlen
(oder Einpunktkompaktifizierung von R); wir bezeichnen sie mit R*. Wen die Vorstellung einer unendlich großen Zahl stört,
der kann die Zahlengerade auf den Einheitskreis projizieren; dem Punkt ∞ entspricht dann der "Nordpol" des Kreises:
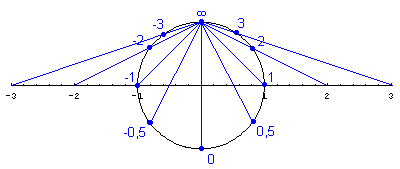
Jetzt können wir untersuchen, ob die Gruppeneigenschaften zutreffen.
- Wenn a und b reelle Zahlen sind, ist offensichtlich a # b auch eine reelle Zahl.
- Wir haben schon oben gesehen, dass # kommutativ und assoziativ ist.
- Aus a # n = a, also 1/a + 1/n = 1/a, folgt 1/n = 0. Das neutrale Element ist daher ∞.
- Das inverse Element zu a ist -a, denn 1/a + 1/(-a) = 0, also a # (-a) = ∞.
Allerdings gibt es zu 0 kein inverses Element, denn wir haben oben gesehen, dass a # 0 immer 0 ergibt. Wir müssen daher
die 0 ausschließen. Das ist aber kein Problem, denn wir haben auch gezeigt, dass a # b nie 0 wird, wenn a und b von 0
verschieden sind. Es ist also auch die Menge R*\{0} gegenüber der Kehrwertaddition abgeschlossen.
Damit haben wir bewiesen:
(R*\{0}, #) ist eine kommutative Gruppe.
Vielleicht findet ja jemand noch mehr Anwendungen für diese Rechenoperation!
Alles Gute bis zum nächsten Mal
Jutta
Zur Homepage -
Archiv der früheren Newsletter
E-mail: gut.jutta.gerhard@chello.at
Newsletter abbestellen
 Welche Seitenlänge hat das Quadrat, das man in ein rechtwinkeliges Dreieck mit den Katheten a und b
einschreiben kann?
Welche Seitenlänge hat das Quadrat, das man in ein rechtwinkeliges Dreieck mit den Katheten a und b
einschreiben kann? Wenn zwei elektrische Widerstände R1 und R2 parallel geschaltet werden, ergibt sich der Gesamtwiderstand R
nach der Formel
Wenn zwei elektrische Widerstände R1 und R2 parallel geschaltet werden, ergibt sich der Gesamtwiderstand R
nach der Formel Ein Gegenstand wird von einer Sammellinse abgebildet. Man kennt die Brennweite f (den Abstand des Brennpunkts von
der Linse) und die Gegenstandweite g (den Abstand des Gegenstands von der Linse). Die Bildweite b kann man
dann nach der sogenannten Linsengleichung berechnen:
Ein Gegenstand wird von einer Sammellinse abgebildet. Man kennt die Brennweite f (den Abstand des Brennpunkts von
der Linse) und die Gegenstandweite g (den Abstand des Gegenstands von der Linse). Die Bildweite b kann man
dann nach der sogenannten Linsengleichung berechnen: Die Erde braucht für einen Umlauf um die Sonne 365 Tage, der Mars 687 Tage. Nach welcher Zeit haben Erde und Mars
wieder die gleiche Stellung zueinander?
Die Erde braucht für einen Umlauf um die Sonne 365 Tage, der Mars 687 Tage. Nach welcher Zeit haben Erde und Mars
wieder die gleiche Stellung zueinander? Seifenblasen haben bekanntlich (wegen der Oberflächenspannung) immer Kugelform. Wenn zwei verschieden große
Seifenblasen mit den Radien r1 und r2 zusammenhängen, nimmt die Trennwand auch die Form
eines Kugelabschnitts (mit Radius r3) an, der sich etwas in die größere Blase hineinwölbt. Dort, wo die Seifenhäute zusmmenstoßen,
bilden sie miteinander Winkel von 120° (weil die Spannungskräfte im Gleichgewicht sein müssen). Man kann zeigen, dass
für die Radien gilt
Seifenblasen haben bekanntlich (wegen der Oberflächenspannung) immer Kugelform. Wenn zwei verschieden große
Seifenblasen mit den Radien r1 und r2 zusammenhängen, nimmt die Trennwand auch die Form
eines Kugelabschnitts (mit Radius r3) an, der sich etwas in die größere Blase hineinwölbt. Dort, wo die Seifenhäute zusmmenstoßen,
bilden sie miteinander Winkel von 120° (weil die Spannungskräfte im Gleichgewicht sein müssen). Man kann zeigen, dass
für die Radien gilt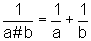 bzw.
bzw.