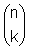gibt an,
auf wieviele verschiedene Arten aus n Elementen k ausgewählt werden können,
wobei es nicht auf die Reihenfolge ankommt.Einige Begriffe aus der Kombinatorik
Der Ausdruck n! (n Fakultät bzw. Faktorielle) gibt an, auf wieviele verschiedene Arten n Elemente angeordnet werden können.
n! = n·(n - 1)· ... ·3·2·1
0! = 1
Beispiel: 6! = 6·5·4·3·2·1 = 720
Berechnung mit dem Taschenrechner: Beim TI-30 X II versteckt sich diese Funktion hinter der Taste PRB (probability).
Der Binomialkoeffizient 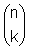gibt an,
auf wieviele verschiedene Arten aus n Elementen k ausgewählt werden können,
wobei es nicht auf die Reihenfolge ankommt.
Beispiel: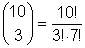 
Wir kürzen durch 7!: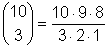 
= 120
Für die praktische Berechnung verwenden wir also besser nicht die obige Formel, sondern folgende Regel:
Im Zähler und im Nenner stehen je k Faktoren. Dabei zählt man im Zähler von n, im Nenner von k hinunter.
Weiters gilt:
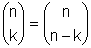
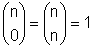
Auf vielen Taschenrechnern heißt die Funktion nCr (combinations). Auch sie versteckt sich beim TI 30-X II hinter der Taste PRB.
Die Binomialkoeffizienten kann man auch aus dem Pascal'schen Dreieck ablesen.
