Home
Ich über mich
Texte
Religion
Mathematik
Spiele
Gästebuch
Home |
Ich über mich |
Texte |
Religion |
Mathematik |
Spiele |
Gästebuch |
Pascal hat dieses Zahlendreieck zwar nicht entdeckt (es war schon den Chinesen als Chu Shun Chiehs Dreieck bekannt), aber als erster systematisch untersucht. Die erste und letzte Zahl jeder Reihe ist 1; die übrigen Zahlen erhält man, indem man jeweils die beiden darüberstehenden Zahlen addiert:
und so weiter...
Die k-te Zahl in der n-ten Reihe (wobei man bei 0 zu zählen anfangen muss) bezeichnet man mit ![]()
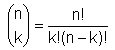 . Dabei bedeutet n! (sprich: "n Fakultät") das Produkt aller natürlichen
Zahlen von 1 bis n, z.B. 4! = 1·2·3·4 = 24.
. Dabei bedeutet n! (sprich: "n Fakultät") das Produkt aller natürlichen
Zahlen von 1 bis n, z.B. 4! = 1·2·3·4 = 24.
Diese Zahlen treten auf, wenn man die Potenzen eines Binoms berechnet (deshalb heißen sie Binomialkoeffizienten):
Z.B.: (a+b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
Sie begegnen uns aber auch in der Wahrscheinlichkeitsrechnung. Sie geben an, auf wie viele Arten man aus einer Menge von n Elementen k auswählen kann, wobei es nicht auf die Reihenfolge ankommt. Daraus folgt: Wenn ein Ereignis mit der Wahrscheinlichkeit p eintritt, so beträgt die Wahrscheinlichkeit, dass es bei n Versuchen k-mal eintritt,
Z.B. ist die Wahrscheinlichkeit, dass man bei 4-maligem Würfeln genau 2 Sechser wirft, 6·(1/6)2·(5/6)2 = 0,1157. Das ist die sogenannte Binomialverteilung.
Am Pascal'schen Dreieck kann man eine Fülle von interessanten Beziehungen entdecken:
 In den Schrägreihen stehen die sogenannten
figurierten Zahlen:
In den Schrägreihen stehen die sogenannten
figurierten Zahlen:
in der ersten Reihe die natürlichen Zahlen (n),
in der zweiten die Dreieckszahlen (D(n) = 1 + 2 + ... + n),
in der dritten die Tetraederzahlen (T(n) = D(1) + D(2) + ... + D(n)) usw.
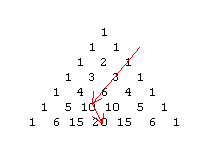 Addiert man die ersten Zahlen einer Schrägreihe, so erhält man die Zahl, die schräg
unter dem letzten Summanden steht.
Addiert man die ersten Zahlen einer Schrägreihe, so erhält man die Zahl, die schräg
unter dem letzten Summanden steht.
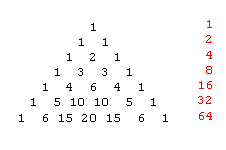 Die Summe der Zahlen in der n-ten Horizontalreihe beträgt 2n
Die Summe der Zahlen in der n-ten Horizontalreihe beträgt 2n
(das kann man leicht beweisen, indem man in der binomischen Formel
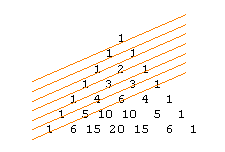 Und wenn man die Zahlen in den "Diagonalen" addiert, erhält man die
Fibonacci-Zahlen.
Und wenn man die Zahlen in den "Diagonalen" addiert, erhält man die
Fibonacci-Zahlen.