Figurierte Zahlen - die Arithmetik der Spielsteinchen

Die Mathematik ist eigentlich aus einem Spiel entstanden. Im 6. Jahrhundert v. Chr. legten die Anhänger des Pythagoras aus Kieselsteinchen regelmäßige Figuren und leiteten daraus die verschiedensten Beziehungen ab. Unsere Wörter "kalkulieren" und "Kalkül" stammen vom lateinischen calculus, Kieselstein.

Schade, dass die Pythagoreer das Pascalsche Dreieck noch nicht kannten (oder etwa doch?). Sonst hätten sie noch mehr Zusammenhänge entdecken können. Dieses Dreieck hat unter anderem folgende Eigenschaft: Die Summe der ersten n Zahlen einer Spalte ist gleich der Zahl, die rechts unter dem letzten Summanden steht. Wenn wir also im Dreieck eine Rechenregel für die Glieder einer Folge gefunden haben, können wir die dazugehörige Reihe (die Summe der ersten n Folgenglieder) leicht erhalten. Wir brauchen nur dieselbe Rechenregel, ein Feld nach rechts unten verschoben, anzuwenden.

Ebene Figuren aus Spielsteinen
Wir bauen Körper
Die vierte Dimension
Literatur und Links

Ebene Figuren aus Spielsteinen

Polygonalzahlen

Wenn wir aufeinanderfolgende natürliche Zahlen addieren, erhalten wir die Dreieckszahlen. Sie heißen so, weil wir die Steinchen in Dreiecksform auslegen können:

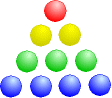D1 = 1 D2 = 1 + 2 = 3 D3 = 1 + 2 + 3 = 6 D4 = 1 + 2 + 3 + 4 = 10

(Die tetraktys, d.h. die 10 als Summe von 1 + 2 + 3 + 4, war für die Pythagoreer die heiligste Zahl überhaupt.)

Die n-te Dreieckszahl ist .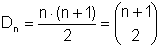
Diese Zahlen finden wir in der 2. Spalte des Pascalschen Dreiecks. Wir können also z.B. ablesen: D₅ = 15.

(Zur Schreibweise: "Zeilen" sind die waagrechten Reihen, "Spalten" die Reihen, die von rechts oben nach links unten verlaufen. Die Zählung beginnt mit der nullten Zeile bzw. Spalte.)

Wir können die Steinchen auch zu Quadraten, Fünfecken, Sechsecken usw. auslegen:

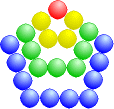
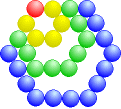
Quadratzahlen: Q1 = 1 Q2 = 1 + 3 = 4 Q3 = 1 + 3 + 5 = 9 Q4 = 1 + 3 + 5 + 7 = 16	Pentagonalzahlen: P1 = 1 P2 = 1 + 4 = 5 P3 = 1 + 4 + 7 = 12 P4 = 1 + 4 + 7 + 10 = 22	Hexagonalzahlen: H1 = 1 H2 = 1 + 5 = 6 H3 = 1 + 5 + 9 = 15 H4 = 1 + 5 + 9 + 13 = 28

Die einzelnen Summanden sind von der Form 1 + m·(n - 1), wobei m um 2 kleiner als die Anzahl der Ecken ist. Das können wir in der (n-1)ten Reihe des Dreiecks ablesen.
Z.B. ist der 5. Summand
bei den Quadratzahlen: 1 + 2·4 = 9
bei den Pentagonalzahlen: 1 + 3·4 = 13
bei den Hexagonalzahlen: 1 + 4·4 = 17

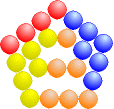
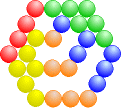
Wenn wir die Steinchen etwas anders einfärben, sieht man, dass wir die Polygonalzahlen auch durch Addition von m Dreieckszahlen zu n erhalten können:

Qn = n + 2·Dn-1 = n + (n - 1)·n = nē	Pn = n + 3·Dn-1	Hn = n + 4·Dn-1

Das können wir in der n-ten Reihe des Pascalschen Dreiecks ablesen (Rechenvorschrift für den n-ten Summanden, nach rechts unten verschoben).
Beispiel: Q₅ = 5 + 2·10 = 25

Die Quadratzahlen erhält man auch durch Addition zweier aufeinanderfolgender Dreieckszahlen:

Q_n = D_n + D_n-1

Beispiel: Q₅ = 15 + 10 = 25

Die Polygonalzahlen sind schon in der Antike gründlich untersucht worden. Einige römische und später auch mittelalterliche Mathematiker haben allerdings geglaubt, dass sie Formeln für den Flächeninhalt von Polygonen darstellen.

Zentrierte Polygonalzahlen

Stellen wir uns vor, dass wir eine Quadratzahl gelegt haben. Nun legen wir in die Mitte jedes kleinen Quadrats noch ein Steinchen. So entstehen die zentrierten Quadratzahlen.

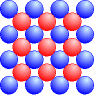ZQ1 = 1 ZQ2 = 4 + 1 = 5 ZQ3 = 9 + 4 = 13 ZQ4 = 16 + 9 = 25

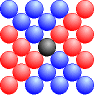Wir können dieses Muster auch erhalten, indem wir um den mittleren Stein 4 Dreiecke legen; die n-te zentrierte Quadratzahl ist daher

ZQ_n = 1 + 4·D_n-1

Beispiel: ZQ₅ = 1 + 4·10 = 41

Ein ähnliches Muster ergibt sich, wenn wir um den mittleren Stein Sechsecke bzw. 6 Dreiecke legen:

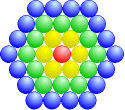Hex1 = 1 Hex2 = 1 + 6 = 7 Hex3 = 1 + 6 + 12 = 19 Hex4 = 1 + 6 + 12 + 18 = 37

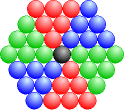Die Zahlen, die auf diese Weise entstehen, bezeichnet man als Hexzahlen. Man kann sie einfacher so berechnen:

Hex_n = 1 + 6·D_n-1

Beispiel: Hex₅ = 1 + 6·10 = 61

Ein solches Muster kennen wir z.B. von Bienenwaben. Es füllt die Ebene dicht aus, wobei die Gesamtlänge der Wände (und damit der Materialverbrauch) so gering wie möglich ist. Die n-te Hexzahl entspricht dann allen Zellen, die vom Zentrum höchstens n Schritte entfernt sind. Eine solche Menge bezeichnet man auch als Nexus; die Hexzahlen sind also die zweidimensionalen Nexuszahlen. (Die eindimensionalen Nexuszahlen sind die ungeraden Zahlen.)

Weiter