Wir bauen Körper

Pyramidalzahlen

Wir können aufeinander folgende Polygone auch zu Pyramiden aufstapeln. Wenn wir z.B. aufeinanderfolgende Dreieckszahlen addieren, erhalten wir die Tetraederzahlen:

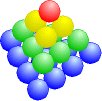T1 = 1 T2 = 1 + 3 = 4 T3 = 1 + 3 + 6 = 10 T4 = 1 + 3 + 6 + 10 = 20

Die n-te Tetraederzahl ist .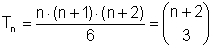
Diese Zahlen stehen in der 3. Spalte des Pascal'schen Dreiecks.

Ebenso können wir quadratische (oder fünfeckige, sechseckige ...) Pyramiden bauen. Wir erhalten etwa für die quadratischen Pyramidalzahlen:

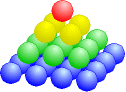Pyr1 = 1 Pyr2 = 1 + 4 = 5 Pyr3 = 1 + 4 + 9 = 14 Pyr4 = 1 + 4 + 9 + 16 = 30

Um diese Zahlen zu berechnen, müssen wir nur unsere Rechenvorschrift für die Polygonalzahlen nach rechts unten verschieben. Die n-te quadratische Pyramidalzahl erhält man z.B. aus

Pyr_n = D_n + 2·T_n-1

(Beispiel: Pyr₅ = 15 + 2·20 = 55)
oder

Pyr_n = T_n + T_n-1

(Beispiel: Pyr₅ = 35 + 20 = 55)

Oktaederzahlen

Natürlich können wir auch aufeinanderfolgende zentrierte Quadratzahlen addieren. Man kann sich das aber besser so vorstellen, dass die "äußeren" Quadrate eine Pyramide und die "inneren" eine etwas kleinere Pyramide bilden. Diese beiden Pyramiden können wir zu einem Oktaeder zusammenbauen:

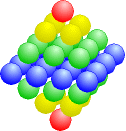Oct1 = 1 Oct2 = 5 + 1 = 6 Oct3 = 14 + 5 = 19 Oct4 = 30 + 14 = 44

Die Rechenvorschrift für die Oktaederzahlen lautet also:

Oct_n = Pyr_n + Pyr_n-1

Wir können aber auch die Vorschrift für die zentrierten Quadratzahlen nach rechts unten verschieben und erhalten:

Oct_n = n + 4·T_n-1

Beispiel: Oct₅ = 5 + 4·20 = 85

Kubikzahlen

Schließlich addieren wir auch aufeinanderfolgende Hexzahlen:

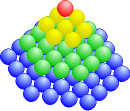K1 = 1 K2 = 1 + 7 = 8 K3 = 1 + 7 + 19 = 27 K4 = 1 + 7 + 19 + 37 = 64

Das sind aber gerade die dritten Potenzen!

Wir können nämlich ein zentriertes Sechseck so umformen, dass es drei Seitenflächen eines Würfels bildet. In dieses "Nest" fügen wir das nächstkleinere Sechseck ein, bis der ganze Würfel fertig ist.

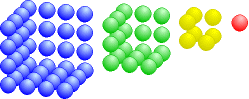
Die Rechenvorschrift für die Kubikzahlen lautet

K_n = n + 6·T_n-1 = n + (n - 1)·n·(n + 1) = n³

Beispiel: K₅ = 5 + 6·20 = 125 = 5³

Zentrierte Kubikzahlen

Wenn wir in jeden Zwischenraum eines Würfels noch ein Steinchen einbauen, erhalten wir die zentrierten Kubikzahlen.

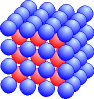ZK1 = 1 ZK1 = 8 + 1 = 9 ZK1 = 27 + 8 = 35 ZK1 = 64 + 27 = 91

Sie sind also die Summe zweier aufeinanderfolgender Kubikzahlen:

ZK_n = K_n + K_n-1 = n + 6·T_n-1 + (n - 1) + 6T_n-2 = 2n - 1 + 6·Pyr_n-1,

das heißt, wir können eine zentrierte Kubikzahl auch erhalten, indem wir zu einer ungeraden Zahl 6 quadratische Pyramiden addieren.
Beispiel: ZK₅ = (4 + 5) + 6·(10 + 20) = 189

Diese Anordnung der Steinchen bezeichnet man als kubisch-raumzentriertes Gitter. Es ist zwar nicht die dichteste Anordnung im Raum, aber die, bei der die Wandfläche zwischen benachbarten Zellen so klein wie möglich ist (so wie bei den Bienenwaben im zweidimensionalen Fall).

Rhombische Dodekaederzahlen

Setzen wir auf jede Seitenfläche eines zentrierten Würfels noch eine quadratische Pyramide, so erhalten wir ein Rhombendodekaeder. (Diese Form tritt in der Natur z.B. bei Granatkristallen auf.)

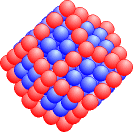Rho1 = 1 Rho2 = 9 + 6·1 = 15 Rho3 = 35 + 6·5 = 65 Rho4 = 91 + 6·14 = 175

Die rhombischen Dodekaederzahlen errechnen sich daher nach der Formel
Rho_n = 2n - 1 + 12·Pyr_n-1
Beispiel: Rho₅ = (4 + 5) + 12·(10 + 20) = 369

Wenn die Steinchen in einem kubisch-raumzentrierten Gitter angeordnet sind, bilden alle Punkte, die vom Zentrum hächstens n Einheiten entfernt sind, ein Rhombendodekaeder. Die rhombischen Dodekaederzahlen sind daher die dreidimensionalen Nexuszahlen.

Zurück - Weiter