Die vierte Dimension

Pentatopzahlen

Wenn wir aufeinanderfolgende Tetraeder in der 4. Dimension aufeinanderstapeln könnten, würden wir den einfachsten vierdimensionalen Körper erhalten, ein sogenanntes Pentatop. Wir können uns das zwar nicht vorstellen, aber die Pentatopzahlen berechnen:

Ptop₁ = 1
Ptop₂ = 1 + 4 = 5
Ptop₃ = 1 + 4 + 10 = 15
Ptop₄ = 1 + 4 + 10 + 20 = 35

Die n-te Pentatopzahl ist .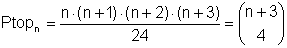
Diese Zahlen stehen in der 4. Spalte des Pascalschen Dreiecks.

Hyperwürfel

Wir können jetzt ebenso aufeinanderfolgende Pyramiden, Würfel usw. addieren. Dazu müssen wir nur die entsprechenden Rechenvorschriften um einen weiteren Schritt nach rechts unten verschieben. Wir wollen das jetzt nur für die rhombischen Dodekaederzahlen durchführen:

Hyp₁ = 1
Hyp₂ = 1 + 15 = 16
Hyp₃ = 1 + 15 + 65 = 81
Hyp₄ = 1 + 15 + 65 + 175 = 256

Das sind die vierten Potenzen (auch Biquadrate genannt)! In der 4. Dimension könnten wir also aufeinanderfolgende Rhombendodekaeder zu Hyperwürfeln zusammenbauen.

Durch Addition von ungeraden Zahlen (eindimensionalen Nexuszahlen) haben wir die Quadratzahlen erhalten, durch Addition von Hexzahlen (zweidimensionalen Nexuszahlen) die Kubikzahlen und durch Addition von rhombischen Dodekaederzahlen (dreidimensionalen Nexuszahlen) die Biquadratzahlen. Wir können auch die 4. Potenzen im Pascalschen Dreieck ablesen.
Beispiel: Hyp₅ = (10 + 15) + 12·(15 + 35) = 625 = 5⁴

Literatur und Links

John H. Conway / Richard K. Guy, Zahlenzauber. Von natürlichen, imaginären und anderen Zahlen. Basel 1997
Aus dem 2. Kapitel dieses Buches habe ich viele Anregungen zu diesem Artikel bekommen.

http://mathworld.wolfram.com/FigurateNumber.html:
Artikel über figurierte Zahlen in Eric Weissteins Online-Enzyklopädie Mathworld, mit vielen Formeln

http://www.wissenschaft-online.de/spektrum/projekt/quasi9.htm:
Seite über platonische Körper (Tetraeder, Würfel, Oktaeder ...); weiter unten wird auch das Rhombendodekaeder vorgestellt. (Spektrum der Wissenschaft)

http://www.uni-duisburg.de/FB9/WET/Medien/f_Gitter.html:
sehr schöne Darstellungen der verschiedenen Kristallgitter. Die Animationen brauchen einige Zeit zum Laden. (Uni Duisburg)

Zurück