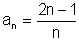
Wir untersuchen die Folge
(Beispielfolge 8).
Zuerst berechnen wir ein paar Folgenglieder, um ein "Gefühl" für den
Verlauf der Folge zu bekommen:
<1, 3/2, 5/3, 7/4, 9/5, ... >
Vermutung: Die Folge ist monoton wachsend. Wir müssen also zeigen:
an £ an+1
für alle n Î N
Um an+1 zu erhalten, ersetzen wir im Bildungsgesetz n durch n+1:
Diese Aussage ist immer wahr, die Vermutung ist daher bewiesen.
(Wir durften die Ungleichung mit n(n+1) multiplizieren, weil dieser Ausdruck für alle natürlichen Zahlen n positiv ist.)
Vermutung: 3 ist obere Schranke.
Diese Aussage stimmt für alle natürliche Zahlen n.
Vermutung: 0 ist untere Schranke.
Auch diese Aussage stimmt für alle natürliche Zahlen n.
Um den Grenzwert der Folge zu berechnen, dividieren wir Zähler und Nenner durch n und wenden die Grenzwertsätze an:
(Wenn in der Termdarstellung auch höhere Potenzen von n vorkommen, dividiert man Zähler und Nenner durch die höchste vorkommende Potenz.)
Ab wann ist |an - 2| < 0,01?
Ab dem 101. Folgenglied ist die Differenz |an - 2| < 0,01.