Folgen und Reihen

Definition und Eigenschaften

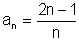
Als (reelle) Zahlenfolge bezeichnet man eine geordnete Folge von Zahlen. Zum Unterschied von Mengen schreibt man Folgen in spitzen Klammern: <a₁, a₂, a₃, ... >
Das n-te Folgenglied schreibt man a_n oder a(n). n heißt Index von a_n. (Manchmal beginnt man die Zählung auch mit a₀.)

Eine Folge kann auf verschiedene Arten dargestellt werden:
man gibt an, wie man aus einem Folgenglied das nächste berechnet (rekursive Darstellung)
oder wie man aus n das n-te Folgenglied berechnet (explizite Darstellung).
Wir können eine Folge also auch als Funktion auffassen:

Eine reelle Zahlenfolge ist eine Funktion N ® R.

Einige Beispiele:

		rekursiv	explizit
(1)	<2, 4, 6, 8, 10, ... >	a1 = 2, an+1 = an + 2	an = 2n
(2)	<10, 9, 8, 7, 6, ... >	a1 = 10, an+1 = an - 1	an = 11 - n
(3)	<10, 20, 40, 80, 160, ... >	a1 = 10, an+1 = 2an	an = 5·2n
(4)	<0,3; 0,03; 0,003; 0,003; ... >	a1 = 0,3; an+1 = an/10	an = 3/10n
(5)	<-1, 1, -1, 1, -1, ... >	a1 = -1, an+1 = -an	an = (-1)n
(6)	<1, 4, 9, 16, 25, ... >	a1 = 1, an+1 = an + 2n + 1	an = n²
(7)	<1, 1/2, 1/3, 1/4, 1/5, ... >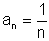
(8)	<1, 3/2, 5/3, 7/4, 9/5, ... >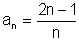

Wichtige Bemerkung

Monotonie:

• Eine Folge <a_n> ist monoton wachsend, wenn die Folgenglieder immer größer werden:

  a_n £ a_n+1       für alle n Î N

• Eine Folge <a_n> ist monoton fallend, wenn die Folgenglieder immer kleiner werden:

  a_n ³ a_n+1       für alle n Î N

Wenn < oder > gilt, spricht man von strenger Monotonie.

Beispiel: Die Folgen (1), (3), (6) und (8) sind (streng) monoton wachsend; (2), (4) und (7) sind (streng) monoton fallend; (5) ist nicht monoton.

Rechenbeispiel zur Monotonie

Schranken:

• Eine Zahl s_o heißt obere Schranke der Folge <a_n>, wenn alle Folgenglieder kleiner oder gleich s_o sind:

  a_n £ s_o       für alle n Î N

• Eine Zahl s_u heißt untere Schranke der Folge <a_n>, wenn alle Folgenglieder größer oder gleich s_u sind:

  a_n ³ s_u       für alle n Î N

• Eine Folge heißt beschränkt, wenn sie eine obere und eine untere Schranke besitzt.

Beispiele:
(1): untere Schranke (z.B.) 0, nach oben unbeschränkt
(2): obere Schranke (z.B.) 10, nach unten unbeschränkt
(7): untere Schranke (z.B.) 0, obere Schranke (z.B.) 1

Rechenbeispiel zur Beschränktheit

Grenzwert und Konvergenz:

Bei manchen Folgen stellen wir fest, dass sich die Folgenglieder einer bestimmten Zahl annähern: (4) und (7) nähern sich 0, (8) nähert sich 2. Diese Zahl heißt Grenzwert oder Limes der Folge:

Die Zahl a heißt Grenzwert der Folge <a_n>, wenn die Differenz |a_n - a| für genügend große n beliebig klein wird.

Man schreibt: lim_n®¥a_n = a (a = Limes von a_n für n gegen unendlich).
Eine Folge, die einen Grenzwert besitzt, heißt konvergent (sie konvergiert bzw. strebt gegen a).
Eine Folge, die keinen Grenzwert besitzt, heißt divergent.

Wenn eine Folge monoton und beschränkt ist, ist sie konvergent.

Beispiel:
Die Folge (7) (a_n = 1/n) konvergiert gegen 0. Die Folgenglieder nehmen zwar nie den Wert 0 an, aber die Differenz |a_n - 0| wird kleiner als jede beliebige Zahl e. Setzen wir z.B. e = 0,01:

Ab dem 101. Folgenglied ist also die Differenz kleiner als 0,01.
Ebenso können wir zu jedem anderen e einen Index n finden, ab dem gilt: |a_n - 0| < e.

Viele Grenzwerte lasen sich mit Hilfe der Grenzwertsätze berechnen:

Sind <an> und <bn> zwei konvergente Folgen mit limn®¥an = a, limn®¥bn = b, so gilt: limn®¥(an + bn) = a + b limn®¥(an - bn) = a - b limn®¥(an·bn) = a·b limn®¥(an/bn) = a/b

Rechenbeispiel zum Grenzwert

Links:
Das mathe online-Applet "Numerische Berechnung von Folgen" (http://www.mathe-online.at/galerie/grenz/grenz.html#folgennumerisch) berechnet Folgenglieder.
Auf der Seite "Calculating and Graphing Sequences" (http://mss.math.vanderbilt.edu/~pscrooke/MSS/sequence.html) kann man sie außerdem graphisch darstellen lassen.

Lernziele: Ich weiß, was eine Folge ist. Ich weiß, was der Grenzwert einer Folge ist.

Übungen

Weiter: Arithmetische und geometrische Folgen, Reihen

Zum Inhaltsverzeichnis