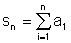 (Summe aller ai für i von 1 bis n).
(Summe aller ai für i von 1 bis n).Bei den Beispielfolgen (1) und (2) erhält man das jeweils nächste Glied, indem man zum vorigen eine (positive oder negative) Konstante k addiert. Eine solche Folge heißt arithmetische Folge. Ihr Bildungsgesetz lautet:
an = a1 + (n-1)·k
Eine arithmetische Folge wird durch eine lineare Funktion dargestellt.
Sie ist für k > 0 monoton wachsend, für k < 0 monoton fallend, in jedem Fall unbeschränkt.
Jedes Folgenglied ist das arithmetische Mittel seiner beiden Nachbarn.
Bei den Beispielfolgen (3), (4) und (5) erhält man das jeweils nächste Glied, indem man das vorige mit einer Konstante q multipliziert. Eine solche Folge heißt geometrische Folge. Ihr Bildungsgesetz lautet:
an = a1·qn-1
Eine geometrische Folge wird durch eine Exponentialfunktion dargestellt.
Sie ist für q > 1 monoton wachsend, für 0 < q < 1 monoton fallend. Ist q < 0,
so sind die Folgenglieder abwechselnd positiv und negativ.
Für |q| < 1 ist die Folge beschränkt und konvergiert gegen 0.
Jedes Folgenglied ist das geometrische Mittel seiner beiden Nachbarn.
Mit dem mathe online-Test "Arithmetisch oder geometrisch?"
Addiert man die Glieder einer Folge, so erhält man eine Reihe. Die Summe
a1 + a2 + ... + an bezeichnet man als n-te Teilsumme sn.
Mit dem Summenzeichen kann man das kürzer schreiben:
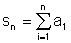 (Summe aller ai für i von 1 bis n).
(Summe aller ai für i von 1 bis n).
(Zur Verwendung des Summenzeichens)
Eine unendliche Reihe ist konvergent, wenn die Folge der Teilsummen konvergiert. Den Grenzwert s bezeichnet man dann als "Summe der unendliche Reihe": s = limn®¥sn
Beispiele:
Arithmetische Reihe:
(Erstes plus letztes Glied mal Anzahl der Glieder, geteilt durch 2)
Geometrische Reihe:
bzw.
Die erste Formel verwendet man für |q| > 1, die zweite für |q| < 1. In diesem Fall konvergiert die Reihe, und wir erhalten die Formel für die Summe der unendlichen geometrischen Reihe:
für |q| < 1.
Links:
Das mathe online-Applet "Numerische Berechnung von Reihen"
Lernziele:
|