Natürliche Exponenten:
Der Graph beschreibt eine S-Kurve und ist symmetrisch zum Koordinatenursprung.
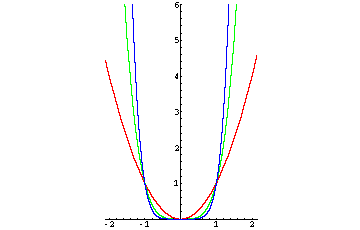
Der Graph ähnelt einer Parabel und ist symmetrisch zur y-Achse.
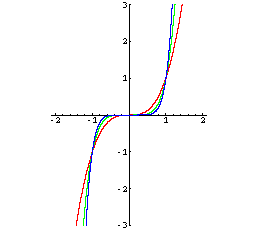
f3: x → x3
f5: x → x5
f7: x → x7
f2: x → x2
f4: x → x4
f6: x → x6
Negative Exponenten:
Der Graph ähnelt einer Hyperbel und ist symmetrisch zum Koordinatenursprung
(für x = 0 nicht definiert!)
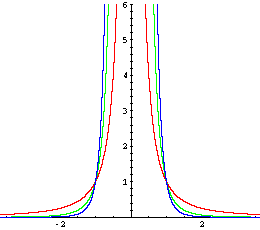
Der Graph ist symmetrisch zur y-Achse
(für x = 0 nicht definiert!)
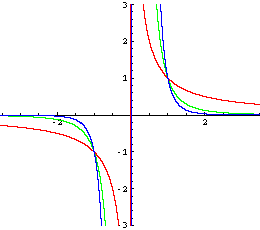
f-1: x → x-1 = 1/x
f-3: x → x-3 = 1/x3
f-5: x → x-5 = 1/x5
f-2: x → x-2 = 1/x2
f-4: x → x-4 = 1/x4
f-6: x → x-6 = 1/x6
Rationale Exponenten (0 < n < 1):
Hier handelt es sich um Wurzelfunktionen. Sie sind nur für x ³ 0 definiert.
Der Graph entsteht, indem man den Graphen der entsprechenden Potenzfunktion an der 1. Mediane spiegelt.
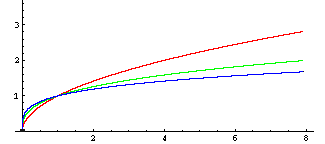
f1/2: x → x1/2 = √x
f1/3: x → x1/3 = 3√x
f1/4: x → x1/4 = 4√x