Beispiele:
| 3x + 1 = 10 | G = N | D = N | L = {3} |
| x² = 4 | G = N | D = N | L = {2} |
| x² = 4 | G = R | D = R | L = {-2, 2} |
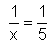 |
G = R | D = R \ {0} | L = {5} |
Einen Ausdruck der Form
T1(x) = T2(x)
nennt man Gleichung mit der Unbekannten x. T1 und T2 sind dabei beliebige
Terme. (Die Unbekannte kann natürlich auch anders benannt werden!)
Je nachdem, welche Zahl man für x einsetzt, erhält man eine wahre oder eine
falsche Aussage.
Grundmenge: alle Zahlen, die zum Einsetzen in die Gleichung vorgesehen sind
Definitionsmenge: alle Elemente der Grundmenge, die für die Unbekannte eingesetzt werden dürfen
Lösungsmenge: alle Elemente der Definitionsmenge, die die Gleichung in eine wahre Aussage überführen
Beispiele:
3x + 1 = 10 G = N D = N L = {3} x² = 4 G = N D = N L = {2} x² = 4 G = R D = R L = {-2, 2} 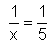
G = R D = R \ {0} L = {5}
Gleichungen, die dieselbe Lösungsmenge haben, heißen äquivalent.
|
Äquivalenzumformungen Die Lösungsmenge einer Gleichung bleibt gleich, wenn man auf beiden Seiten
|
Wir werden immer versuchen, eine Gleichung durch Äquivalenzumformungen auf die einfachste Form zu bringen.
Dabei können Sonderfälle auftreten, z.B.:
x = x
Diese Aussage ist für alle Zahlen wahr ⇒ L = Dx = x + 1
Diese Aussage ist für alle Zahlen falsch ⇒ L = { }
Genauere Erklärungen: mathe online, Gleichungen
http://www.mathe-online.at/mathint/gleich/i.html
Abschnitte "Gleichung" - "Äquivalenzumformungen"
Eine Gleichung der Form
ax + b = 0
mit a, b ∈ R, a ≠ 0
heißt lineare Gleichung (d.h., x kommt nur in der ersten Potenz vor).
Sie hat in R genau eine Lösung: L = {-b/a}
Beispiel:
(Wenn nicht anders angegeben, ist die Grundmenge immer R)
7x - 6
= 4x + 9 | - 4x 3x - 6
= 9 | + 6 3x
= 15 | :3 x
= 5 L = {5}
Lernziele:
|
Genauere Erklärungen: mathe online, Gleichungen
http://www.mathe-online.at/mathint/gleich/i.html
Abschnitte "Lineare Gleichungen", "Normalform der linearen Gleichung"
Weiter: Quadratische Gleichungen