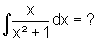
Wir substituieren t = x² + 1 und leiten ab:
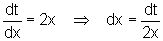
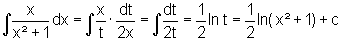
Partielle Integration
Durch Umformen der Produktregel erhält man
∫f'(x)·g(x)dx = f(x)·g(x) - ∫f(x)·g'(x)dx
Als f'(x) wählt man eine Funktion, die beim Integrieren nicht komplizierter wird, z.B. ex, sin x, cos x.
Beispiele:
∫x·cos x dx = ?
Wir setzen f'(x) = cos x, g(x) = x:
∫x·cos x dx = x·sin x - ∫1·sin x dx = x·sin x + cos x + c∫ln x dx = ?
Trick: f'(x) = 1, g(x) = ln x
∫1·ln x dx = x·ln x - ∫x·1/xdx = x·ln x - x + c
Integration durch Substitution
Aus der Kettenregel erhält man
∫f(g(x))·g'(x)dx = F(g(x))
Wenn wir g(x) durch t ersetzen (substituieren), können wir auch schreiben: ∫f(t)dt = F(t).
Beachte, dass man auch dx durch dt ausdrücken muss!
Beispiel:
Wir substituieren t = x² + 1 und leiten ab:
Bei einem bestimmten Integral ändern sich auch die Integrationsgrenzen. Dadurch erspart man sich die Rücksubstitution am Ende.
Beispiel:
Substitution: t = sin x; neue Grenzen: sin 0 = 0, sin π/2 = 1
Wenn die innere Funktion linear ist, vereinfacht sich die Berechnung. Man kann dann einfach die Stammfunktion durch die innere Ableitung dividieren:
∫f(ax + b)dx = 1/a·F(ax + b)
Beispiel: ∫e5x-1dx = 1/5·e5x-1 + c
Abschließende Bemerkung:
"Differenzieren ist ein Handwerk, Integrieren eine Kunst." Es ist nicht immer auf den ersten Blick sichtbar,
welche Integrationsmethode zum Ziel führt. Oft muss man mehrere Möglichkeiten durchprobieren.
Es gibt auch Funktionen, die nicht elementar integrierbar sind, z.B. die in der Wahrscheinlichkeitsrechnung
wichtige Normalverteilungsfunktion: f(x) = e-x²/2.
|
Lernziele:
|