Kurvendiskussionen

(Polynomfunktionen)

Mithilfe der Differentialrechnung können wir Funktionsgraphen untersuchen: Wo ist die Funktion steigend bzw. fallend, wo gibt es besondere Punkte wie Hochpunkte, Tiefpunkte, Wendepunkte?

Vorbemerkung 1:
Wenn wir den Funktionswert zu einem gegebenen x suchen, müssen wir x in die ursprüngliche Funktion einsetzen.
Wenn wir die Steigung an einer gegebenen Stelle suchen, müssen wir x in die 1. Ableitung einsetzen.

Vorbemerkung 2 (für Profis):
f(x) soll im Folgenden immer eine zweimal stetig differenzierbare Funktion sein.

Die Bedeutung der 1. Ableitung

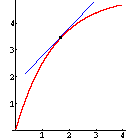
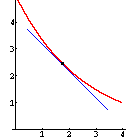
Die 1. Ableitung gibt die Änderung des Funktionswertes an, d.h. die Steigung des Funktionsgraphen an einer bestimmten Stelle.

Ist f'(x) > 0, ist die Funktion monoton steigend.
Ist f'(x) < 0, ist die Funktion monoton fallend.
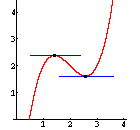
Ist f'(x) = 0, hat der Graph an dieser Stelle eine waagrechte Tangente. Es kann sich um einen Hochpunkt oder Tiefpunkt handeln ...
aber auch um einen Wendepunkt mit einer waagrechten Tangente. Um das zu entscheiden, brauchen wir die 2. Ableitung.

Die Bedeutung der 2. Ableitung

Die 2. Ableitung gibt die Änderung der Steigung an. Sie gibt also Auskunft über die Krümmung des Graphen.

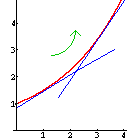Ist f''(x) > 0, wird die Steigung größer.
Die Kurve ist daher linksgekrümmt (positiv gekrümmt, konvex).
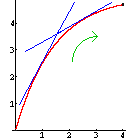Ist f''(x) < 0, wird die Steigung kleiner.
Die Kurve ist daher rechtsgekrümmt (negativ gekrümmt, konkav).
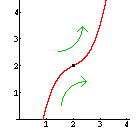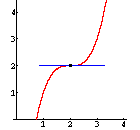
Bei einem Wendepunkt ändert sich die Krümmung. An dieser Stelle ist f''(x) = 0.
(Zur Sicherheit sollte man noch überprüfen, ob f'''(x) ¹ 0 ist - sonst kann es sich auch um einen Flachpunkt handeln.)

Besondere Punkte des Graphen

Aus diesen Überlegungen empfiehlt sich folgendes Vorgehen bei Kurvendiskussionen:

Schnittpunkt mit y-Achse x = 0
Nullstellen
(Schnittpunkte mit x-Achse)		 f(x) = 0
Extremwerte f'(x) = 0
Die gefundenen Werte für x werden in die 2. Ableitung eingesetzt:
f''(x) > 0: Tiefpunkt
f''(x) < 0: Hochpunkt
Wendepunkt f''(x) = 0, f'''(x) ¹ 0
Die Steigung der Wendetangente erhält man - wie die Steigung jeder beliebigen Tangente - durch Einsetzen von x in die 1. Ableitung.

Symmetrieeigenschaften

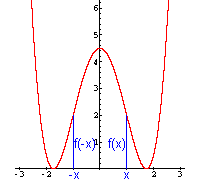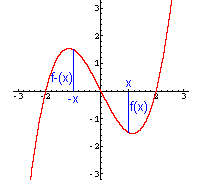
Wenn nur gerade Potenzen von x (und eventuell eine Konstante) vorkommen, gilt für alle x:
f(-x) = f(x)
Eine solche Funktion nennt man gerade Funktion.
Ihr Graph ist symmetrisch zur y-Achse.
Wenn nur ungerade Potenzen von x vorkommen, gilt für alle x:
f(-x) = -f(x)
Eine solche Funktion nennt man ungerade Funktion.
Ihr Graph ist symmetrisch zum Koordinatenursprung.

Lernziele:

  • Ich kann die Nullstellen, Extremwerte und Wendepunkte einer Polynomfunktion berechnen.
  • Ich kann den Graphen einer Polynomfunktion und seine besonderen Punkte zeichnen.
  • Ich kann die Gleichung der Tangente an einen beliebigen Punkt des Graphen bestimmen.
  • Ich kann anhand der Funktionsgleichung feststellen, ob der Graph symmetrisch ist.

Musterbeispiel

Übungen

Weiter: Umkehraufgaben

Zum Inhaltsverzeichnis