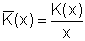
(Ableitung der Kostenfunktion)
Die Betriebskostenfunktion oder einfacher Kostenfunktion eines Unternehmens gibt an, wieviel die Produktion einer bestimmten Menge kostet. Dabei gibt man die Menge meist in Mengeneinheiten (ME) und die Kosten in Geldeinheiten (GE) an.
| K(x) | Betriebskostenfunktion: Kosten für die Produktion von x ME |
|
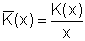Stückkostenfunktion: durchschnittliche Kosten für eine ME |
| K'(x) | Grenzkostenfunktion: zusätzliche Kosten, wenn eine ME mehr produziert wird (Ableitung der Kostenfunktion) |
Die Kostenfunktion ist immer monoton wachsend. Sie besteht aus den Fixkosten (Kfix = K(0), von der Menge unabhängig) und den variablen Kosten (Kvar(x) = K(x) - K(0)).
Einige typische Kostenverläufe (rot) mit Stückkosten (grün) und Grenzkosten (blau):
 |
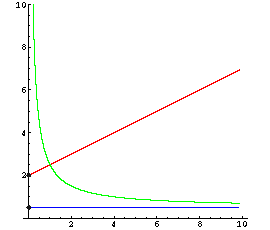linear: Grenzkosten sind konstant K'' = 0 |
 |
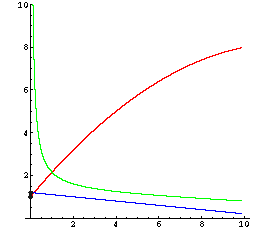degressiv: Grenzkosten werden niedriger K'' < 0 |
 |
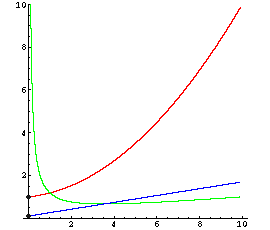progressiv: Grenzkosten werden höher K'' > 0 |
 |
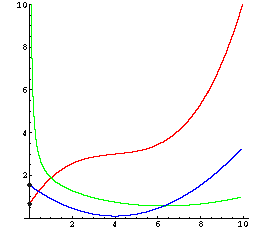In der Praxis ergibt sich meist ein gemischter Kostenverlauf: Die Grenzkosten werden zuerst niedriger, ab einer bestimmten Menge (Kostenkehre) wieder höher. Die Kostenkehre ist der Wendepunkt der Kostenfunktion, man erhält sie aus K''(x) = 0. |
Das Betriebsoptimum ist das Minimum der Stückkostenfunktion, d.h. die Menge, bei der der Betrieb am rentabelsten produziert. Man erhält es aus der Gleichung
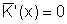bzw.
.
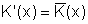Beispiel: Ein Betrieb hat die Kostenfunktion
K(x) = 0,1x² + 2x + 40 (Kfix = 40, Kvar(x) = 0,1x² + 2x; progressiver Kostenverlauf)
K'(x) = 0,2x + 2Aus der Gleichung
xopt = 20
Bei einer Produktion von 20 ME sind also die Stückkosten am niedrigsten, nämlich. Das ist gleichzeitig die langfristige Preisuntergrenze (kostendeckender Preis): der Betrieb muss sein Produkt zu einem Preis von mindestens 6 GE verkaufen, damit er kostendeckend produzieren kann.
(Die kurzfristige Preisuntergrenze ist das Minimum der variablen Stückkosten Kvar(x)/x. Das wollen wir hier nicht berechnen.)
