Erlös und Gewinn bei vollständiger Konkurrenz
Wenn der Markt sehr groß ist, hat der einzelne Anbieter praktisch keinen Einfluss auf den
Preis. (Ein einzelner Bauer hat keinen Einfluss auf den Milchpreis.) Wir können vereinfachend
annehmen, dass er eine beliebige Menge zu einem konstanten Verkaufspreis absetzen kann.
| p |
Verkaufspreis pro ME |
| E(x) = px |
Erlösfunktion (Umsatz) |
| G(x) = E(x) - K(x) |
Gewinnfunktion |
(Auf den folgenden Bildern ist der Graph der Kostenfunktion rot, der Graph der Erlösfunktion
blau dargestellt.)
 |
Bei linearem Kostenverlauf schneiden einander die Graphen
von Kosten- und Erlösfunktion in einem Punkt (vorausgesetzt, der Preis ist höher
als die Grenzkosten). Dieser Schnittpunkt entspricht der Gewinnschwelle
(Break-even-point). Unterhalb davon macht der Betrieb Verlust, darüber Gewinn.
Es ist daher am günstigsten, die Produktionskapazität voll auszunützen.
Analoges gilt bei degressivem Kostenverlauf. |
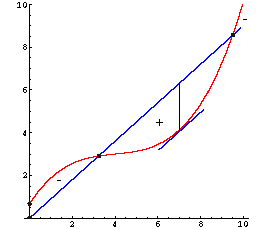 |
Bei progressivem oder gemischten Kostenverlauf
haben die Graphen zwei Schnittpunkte, die Gewinngrenzen. Nur im Bereich
dazwischen macht der Betrieb Gewinn,
darüber oder darunter fährt er Verluste ein.
Der Produzent wird versuchen, den maximalen Gewinn zu erzielen. |
Die Gewinngrenzen erhält man aus der Gleichung
G(x) = 0 bzw.
E(x) = K(x),
das Maximum der Gewinnfunktion aus
G'(x) = 0 bzw.
E'(x) = K'(x)
E'(x) = p, also ist der Gewinn maximal, wenn die Grenzkosten gleich dem Verkaufspreis sind
(d.h., die Tangente an den Graphen von K(x) ist zum Graphen von E(x) parallel).
|
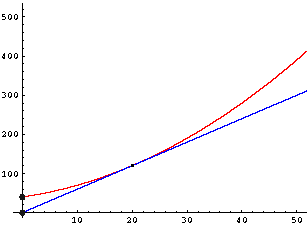
Beispiel:
Angenommen, der Produzent aus dem vorigen Beispiel kann seinen Artikel um 6 GE verkaufen.
Dann lautet die Gewinnfunktion:
G(x) = 6x - (0,1x² + 2x + 40) = -0,1x² + 4x - 40
Die Gleichung E(x) = K(x) (bzw. G(x) = 0) hat nur eine
Lösung bei x = 20, also beim Betriebsoptimum.
Bei dieser Produktionsmenge macht der Betrieb gerade keinen Verlust, es handelt sich
um einen sogenannten Grenzbetrieb.
Wie man aus der Zeichnung sieht, kann man das Betriebsoptimum graphisch ermitteln,
indem man vom Koordinatenursprung eine Tangente an den Graphen von K(x) legt. |
 |
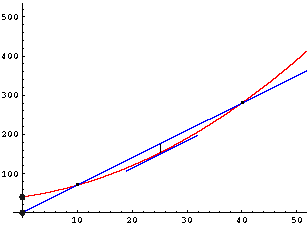
Wenn der Verkaufspreis 7 GE beträgt, lautet die Gewinnfunktion:
G(x) = 7x - (0,1x² + 2x + 40) = -0,1x² + 5x - 40
Die Gleichung E(x) = K(x) (bzw. G(x) = 0) hat die
Lösungen x1 = 10, x2 = 40.
Das sind die Gewinngrenzen.
Die Lösung der Gleichung E'(x) = K'(x) (bzw. G'(x) = 0)
ist x = 25. Der Betrieb erzielt also den maximalen
Gewinn bei einer Produktion von 25 ME, und zwar beträgt der Gewinn G(25) = 22,5 GE. |
 |
Übungen
Weiter: Angebot und Nachfrage
Zum Inhaltsverzeichnis



