Definition von Georg Cantor (1845 - 1918): "Eine Menge ist eine Zusammenfassung wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens (genannt die Elemente der Menge) zu einem Ganzen."
Man kann eine Menge beschreiben oder ihre Elemente aufzählen (in geschwungenen Klammern { }, die Reihenfolge ist dabei egal).
Beispiele:
Ö = Menge aller österreichischen Bundesländer
Ö = {Burgenland, Kärnten, Niederösterreich, Oberösterreich, Salzburg, Steiermark, Tirol, Vorarlberg, Wien}
A = {x ∈ N / x ≤ 7} ... Menge aller natürlichen Zahlen kleiner oder gleich 7
A = {1, 2, 3, 4, 5, 6, 7}
B = {x ∈ Ng / 4 ≤ x ≤ 12} ... Menge aller geraden Zahlen zwischen 4 und 12
B = {4, 6, 8, 10, 12}
Wichtige Begriffe und Zeichen:
|
∈ |
Element |
in obigem Beispiel: Salzburg ∈
Ö, Bayern Ï
Ö |
|
{ } |
leere Menge |
Menge die keine Elemente enthält |
|
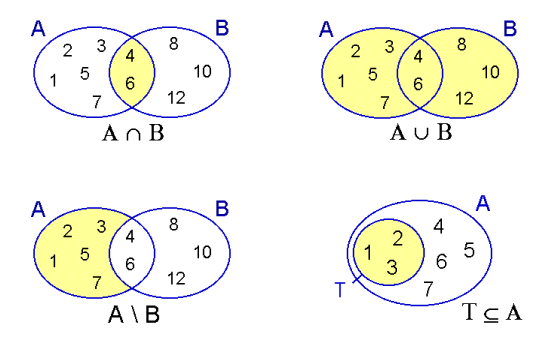
⊆ |
Teilmenge |
Menge, die ganz in einer anderen enthalten ist |
|
A ∩ B |
Durchschnitt |
alle Elemente, die in A und B enthalten sind |
|
A ∪ B |
Vereinigung |
alle Elemente, die in A oder B enthalten sind |
|
A \ B |
Differenzmenge |
alle Elemente von A, die nicht in B enthalten sind |
|
A' |
Komplementärmenge |
Ist A eine Teilmenge der Grundmenge M, so bezeichnet man M \ A auch als Komplementärmenge von A. |
Darstellung durch Mengendiagramme:

Eine Teilmenge von R in der Art von
I = {x ∈ R / 2 ≤ x ≤ 5}
(alle reellen Zahlen zwischen 2 und 5 einschließlich)
kann man nicht mehr aufzählen. Solche Mengen bezeichnet man als Intervalle; man schreibt auch
I = [2, 5]
Darstellung auf der Zahlengeraden:
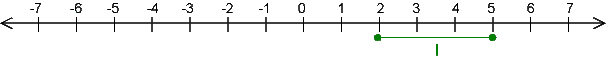
|
[a, b] = {x ∈R / a ≤ x ≤ b} |
abgeschlossenes Intervall (Endpunkte gehören dazu) |
|
]a, b[ = {x ∈R / a < x < b} |
offenes Intervall (Endpunkte gehören nicht dazu)andere Schreibweise: (a, b) |
|
[a, ∞[ = {x ∈ R / x ≥ a} |
unbeschränktes Intervall (da ∞ (unendlich) keine Zahl ist, ist dieses Intervall rechts offen!) |
Nähere Informationen unter http://www.mathematik.net/mengen/12.htm, http://members.aol.com/SteffMath/Mengenlehre.html
Lernziele:
|