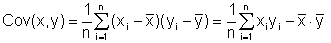
("Mittelwert der Produkte minus Produkt der Mittelwerte")
Oft werden zwei Merkmale daraufhin untersucht, wie stark sie miteinander zusammenhängen (korrelieren). Ein Maß dafür ist die Kovarianz:
("Mittelwert der Produkte minus Produkt der Mittelwerte")
Bei der Methode der linearen Regression nimmt man an, dass zwischen den beiden
Werten ein linearer Zusammenhang besteht, das heißt:
y = ax + b + ein zufälliger Fehler
Die Konstanten a und b werden so bestimmt, dass die Summe der Quadrate der Fehler möglichst klein
wird (Methode der kleinsten Fehlerquadrate von C.F. Gauß).
Anschaulich können wir uns das so vorstellen, dass wir x und y als Koordinaten von Punkten
auffassen und in ein Koordinatensystem einzeichnen. Wir suchen dann die Gerade,
die diese Punktwolke am besten annähert (Regressionsgerade, siehe
Beispiel). Diese Aufgabe kann man mit Hilfe der Differentialrechnung
lösen und erhält als Gleichung der Regressionsgeraden:
y = ax + b, wobei
Die zweite Formel ergibt sich daraus, dass die Regressionsgerade durch den "Schwerpunkt"
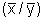der Punktwolke geht.
Der Korrelationskoeffizient r liefert ein Mass dafür, wie gut die gegebenen Werte durch diese lineare Funktion angenähert werden. Er ist definiert durch
Der Wert von r liegt immer zwischen -1 und 1. Dabei bedeutet
r nahe bei 1: starke positive Korrelation (je größer x, umso größer y)
r nahe bei -1: starke negative Korrelation (je größer x, umso kleiner y)
r nahe bei 0: schwacher oder gar kein Zusammenhang
Manchmal verwendet man auch das Bestimmtheitsmaß r². Es gibt an, welcher Anteil der Abweichungen vom Mittelwert durch die Korrelation erklärt wird.
In manchen Fällen kann es zweckmäßiger sein, die gegebenen Daten durch eine quadratische Funktion, eine Exponentialfunktion usw. anzunähern. Dann spricht man von quadratischer Regression bzw. exponentieller Regression. Diese Fälle wollen wir hier nicht behandeln.
Beispiel:
Wir wollen anhand der Angaben aus dem vorigen Beispiel untersuchen, inwieweit Körpergröße (x) und Schuhgröße (y) zusammenhängen. Wir zeichnen die Werte in ein Koordinatensystem:
Zur Ermittlung der Regressionsgeraden machen wir am besten eine Tabelle:
i
xi
yi
xi²
yi²
xi·yi
1
168
39
28224
1521
6552
2
170
39
28900
1521
6630
3
161
38
25921
1444
6118
4
168
38
28224
1444
6384
5
162
37
26244
1369
5994
6
172
41
29584
1681
7052
7
164
38
26896
1444
6232
8
167
38
27889
1444
6346
9
170
40
28900
1600
6800
10
158
37
24964
1369
5846
Summe
1660
385
275746
14837
63954
: n =
166
38,5
27574,6
1483,7
6395,4
V(x) = 27574,6 - 166² = 18,6
V(y) = 1483,7 - 38,5² = 1,45
Cov(x,y) = 6395,4 - 166·38,5 = 4,4a = 4,4/18,6 = 0,237
b = 38,5 - 0,237·166 = -0,769
r = 4,4/√(18,6·1,45) = 0,847Die Gleichung der Regressiongeraden lautet also
y = 0,237x - 0,769
Der Korrelationskoeffizient liegt nahe bei 1, es handelt sich also um einen starken positiven Zusammenhang.
Achtung: Eine starke Korrelation muss noch keinen ursächlichen Zusammenhang bedeuten! (Es gibt zwar eine positive Korrelation zwischen der Anzahl der Störche im Burgenland und der Zahl der Geburten, aber daraus kann man nicht schließen, dass der Storch die Kinder bringt!)
Mithilfe der linearen Regression kann man auch einen Trend abschätzen. Das ist vor allem dann von Bedeutung, wenn es sich bei den Daten um eine Zeitreihe handelt.
Beispiel:
Der PKW-Bestand in Österreich betrug (in Tausend):
1970: 1197
1975: 1721
1980: 2247
1985: 2531
1990: 2991
Erstelle eine Prognose für 2000!
Wenn wir 1970 als Jahr 0 annehmen, lautet die Gleichung der Regressionsgeraden:
y = 87,96x + 1257,8Für 2000 (Jahr 30) erhalten wir dann den Wert
y(30) = 87,96·30 + 1257,8 = 3896,6Wir können also für 2000 einen PKW-Bestand von 3896600 erwarten (blauer Punkt). Tatsächlich waren es 4097000 PKW, die Prognose ist also ziemlich gut.
