Die Definitionen aus dem vorigen Abschnitt sind nur sinnvoll für Winkel zwischen 0° und 90°. Die folgende Definition gilt für beliebige Winkel:
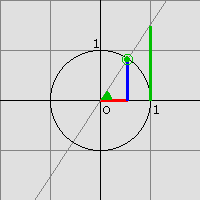
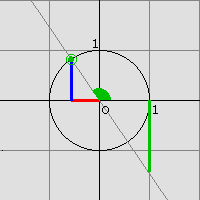
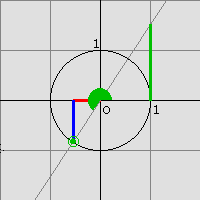
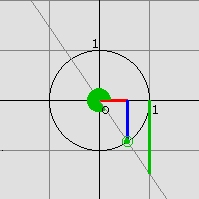
Wir zeichnen einen Kreis um den Koordinatenursprung mit dem Radius 1 und eine Gerade durch den Koordinatenursprung, die mit der positiven x-Achse den Winkel α einschließt. Der Schnittpunkt dieser Geraden mit dem Einheitskreis hat dann die Koordinaten (cos α / sinα), der Schnittpunkt mit der Tangente in (1/0) hat die Koordinaten (1 / tan α). Man kann also die Werte der Winkelfunktionen wie auf den Abbildungen ablesen (blau: sin α, rot: cos α, grün: tan α). Dabei muss auch auf das Vorzeichen geachtet werden.




(Überlege dir, dass diese Definitionen für 0° < α < 90° mit denen aus dem vorigen Abschnitt übereinstimmen!)
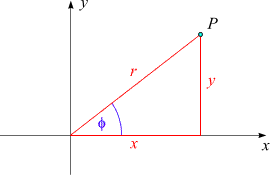
Die Lage eines Punktes in der Ebene kann man auch durch seinen Abstand zum Koordinatenursprung (r) und seinen Richtungswinkel (φ = Winkel zwischen r und der positiven x-Achse) angeben. Mit den folgenden Formeln kann man zwischen kartesischen Koordinaten und Polarkoordinaten umrechnen:
x = r·cos(φ) y = r·sin(φ) |
r = √(x² + y²) tan(φ) = y/x |
Beispiele:
Die Polarkoordinaten sind gegeben: P(10; 60°)
x = 10·cos(60°) = 5, y = 10·sin(60°) = 8,66
Die kartesischen Koordinaten von P sind also P(5 / 8,66).Die kartesischen Koordinaten sind gegeben: Q(-4 / 3)
r = √((-4)² + 3²) = 5, tan-1(-3/4) = -36,87°
Da der Punkt Q im zweiten Quadranten liegt (d.h. 90° < φ < 180°), muss man zu diesem Wert 180° addieren: φ = 143,13°
Die Polarkoordinaten lauten also Q(5; 143,13°).
Beachte, dass für r = 0, also für den Koordinatenursprung selbst, der Winkel nicht definiert ist. Weitere Informationen siehe mathe online, Ebene Polarkoordinaten und das dazupassende Applet.
Nun können wir die Graphen der Winkelfunktionen zeichnen (blau: Sinus, rot: Cosinus, grün: Tangens). Als x-Werte verwenden wir dabei das Bogenmaß der Winkel, d.h. die Länge des entsprechenden Kreisbogens im Einheitskreis (siehe dazu mathe online, Das Bogenmaß).
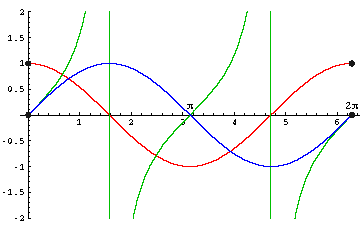
Für Winkel unter 0 oder über 2π (= 360°) wiederholen sich die Funktionswerte immer wieder. Man bezeichnet solche Funktionen als periodische Funktionen.
Applets zu diesem Thema:
mathe online, Die Graphen von sin, cos und tan
"Six Trig Functions"
Lernziele:
|